Численное решение переопределенных СЛАУ. Метод наименьших квадратов

3.2. Понятие о методах решения плохо обусловленных СЛАУ

Улучшить качество численного решения СЛАУ метода наименьших квадратов возможно, если использовать различные преобразования матрицы

Большинство прямых методов решения линейных систем основано либо на замене исходной системы 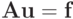( — квадратная матрица) на эквивалентную либо на представлении матрицы в виде произведения других матриц, таких, чтобы новая система либо решалась более просто, либо была лучше (по крайней мере, не хуже) обусловлена, чем исходная.

Подход, использующий спектральную эквивалентность матриц и (в смысле границ спектра собственных значений), основан на умножении на близкую в некотором смысле матрицу 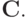Последняя матрица выбирается таким образом, чтобы произведение было близким к единичной матрице (при этом 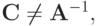так как обращение плохо обусловленной матрицы приводит к накоплению вычислительных ошибок. Число обусловленности матрицы будет близко к единице. Метод энергетически эквивалентных операторов оказался эффективным при численном решении сеточных уравнений при разностной аппроксимации уравнений в частных производных эллиптического типа.

Идея предобусловливания СЛАУ состоит в том, чтобы вместо исходной системы 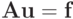решать систему где матрица выбирается так, чтобы она была симметричной положительной, хорошо обусловленной.

Определение. Матрица с вещественными элементами q_ij является ортогональной, если

Пусть матрица невырождена. Тогда она представима в виде

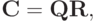
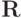где — ортогональная, а — верхняя треугольная матрицы. В качестве матрицы часто используется симметричная ортогональная матрица :

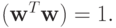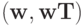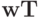где - произвольный вектор - столбец, такой, что Матрица есть произведение вектора - столбца на вектор - строку (преобразование Хаусхолдера или метод отражений ).

Заметим, что симметричность матрицы (матрицы отражений) показывается непосредственной проверкой; ортогональность можно показать следующим образом:

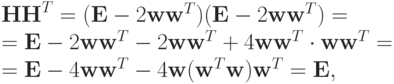
так как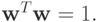

Матрица СЛАУ представляется в виде 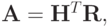после чего решается эквивалентная система уравнений