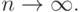НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 4: Численное решение переопределенных СЛАУ. Метод наименьших квадратов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3914 / 1195 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

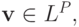Теорема. Пусть столбцы матрицы $\mathbf{A}$ линейно независимы, т.е. ранг $\mathbf{A}$ равен p. Тогда существует единственный элемент p - мерного евклидова пространства $\mathbf{v} \in L^P,$ являющийся обобщенным решением системы (3.2), и решением СЛАУ

${\mathbf{A}}^*{\mathbf{BAu}} = {\mathbf{A}}^*{\mathbf{Bf}},$

( 3.5)

состоящей из p скалярных уравнений относительно неизвестных $\left\{{\mathbf{u}_k}\right\}_{k = 1}^{k = p},$ доставляющий минимум квадратичной форме

$\Phi (\mathbf{u}) = {\left[\mathbf{Au} - \mathbf{f}, \mathbf{Au} - \mathbf{f}\right]}^n.$

Доказательство.

Покажем, что решение СЛАУ 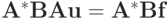${\mathbf{A}}^*{\mathbf{BAu}} = {\mathbf{A}}^*{\mathbf{Bf}}$ существует и единственно. Введем обозначение ${\mathbf{q}}_k \in L^n$ для вектора — k столбца матрицы системы $\mathbf{A}$ :

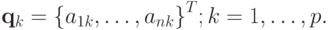
${\mathbf{q}}_k = {\{a_{1k}, \ldots, a_{nk} \}}^T; k = 1, \ldots, p.$

Несложно показать, что матрица $\mathbf{D} = {\mathbf{A}}^*{\mathbf{BA}}$ системы (3.5) есть квадратная матрица p x p. 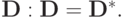Элемент d_ij этой матрицы, стоящий на пересечении i строки и j столбца, есть $d_{ij} = {({\mathbf{q}}_i, {\mathbf{Bq}}_j)}^n = {({\mathbf{Bq}}_i,{\mathbf{q}}_j)}^n = {\left[{{\mathbf{q}}_i,{\mathbf{q}}_j}\right]}^n,$ в силу коммутативности скалярного произведения d_ij = d_ij, что означает самосопряженность матрицы $\mathbf{D}: \mathbf{D} = {\mathbf{D}}^*.$

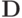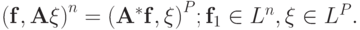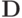Покажем, что матрица $\mathbf{D}$ невырождена и положительно определена. Напомним, что ${(\mathbf{f},\mathbf{A\xi })}^n = {({\mathbf{A}}^*{\mathbf{f}},{\mathbf{\xi }})}^P; {\mathbf{f}}_1 \in L^n, \mathbf{\xi } \in L^P.$ Это равенство проверяется непосредственно, если записать обе его части в развернутом виде. Невырожденность матрицы $\mathbf{D}$ следует из того, что ранг матрицы $\mathbf{A}$ равен p.

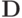В таком случае $0 < {\left[{\mathbf{Ax},\mathbf{x}}\right]}^n = {(\mathbf{BAx},\mathbf{Ax})}^n = {({\mathbf{A}}^*{\mathbf{BAx}},{\mathbf{x}})}^p = {(\mathbf{Dx},\mathbf{x})}^p.$ Поскольку $\mathbf{D}$ невырождена и положительно определена, то (3.5) имеет единственное решение 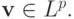$\mathbf{v} \in L^p.$ Теперь покажем, что $\mathbf{v}$ — единственное обобщенное решение системы. Для любого вектора $\mathbf{\Delta } \ne 0$ выполнено 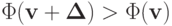$\Phi (\mathbf{v} + \mathbf{\Delta }) > \Phi (\mathbf{v})$ :

$\Phi (\mathbf{v} + \mathbf{\Delta }) = {\left[{\mathbf{A}(\mathbf{v} + \mathbf{\Delta }) - \mathbf{f},\mathbf{A}(\mathbf{v} + \mathbf{\Delta }) - \mathbf{f}}\right]}^n = \\ = {\left[{\mathbf{Av} - \mathbf{f},\mathbf{Av} - \mathbf{f}}\right]}^n - 2{\left[{\mathbf{Av} - \mathbf{f},\mathbf{A\Delta }}\right]}^n + {\left[{\mathbf{A\Delta },\mathbf{A\Delta }}\right]}^n = \\ = \Phi (\mathbf{v}) + {2\left[{\mathbf{Av} - \mathbf{f},\mathbf{A\Delta }}\right]}^n + {(\mathbf{D\Delta },\mathbf{\Delta })}^p = \Phi (\mathbf{v}) + {(\mathbf{D\Delta },\mathbf{\Delta })}^p > \Phi (\mathbf{v}),$

что и требовалось доказать.

При доказательстве использовалось

${\left[{\mathbf{Av} - \mathbf{f},\mathbf{A\Delta }}\right]}^n = {(\mathbf{B}(\mathbf{Av} - \mathbf{f}),\mathbf{A\Delta })}^n = {({\mathbf{A}}^*{\mathbf{BAv}} - {\mathbf{A}}^*{\mathbf{Bf}},\mathbf{\Delta })}^p = 0,$

поскольку 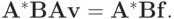${\mathbf{A}}^*{\mathbf{BAv}} = {\mathbf{A}}^*{\mathbf{Bf}}.$

Так как матрица $\mathbf{D} = {\mathbf{A}}^*{\mathbf{BA}}$ — симметричная и положительно определенная, то для численного решения полученной СЛАУ можно воспользоваться итерационными методами.

Если система векторов 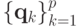$\left\{{{\mathbf{q}}_k}\right\}_{k = 1}^p$ оказывается ортонормированной, т.е. $[{\mathbf{q}}_i,{\mathbf{q}}_j ] = \delta_{ij} i,j = 1, \ldots, p,$ то матрица $\mathbf{D}$ оказывается единичной. Ее элементы и есть скалярные произведения $[{\mathbf{q}}_i,{\mathbf{q}}_j ].$ В этом случае решением системы будет

$\mathbf{u} = \mathbf{A^*Bf}.$

Следует отметить, что если базисные функции 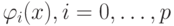$\varphi_i (x), i = 0, \ldots, p$ не выбираются специальным образом, то при достаточно больших p 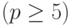$(p \ge 5)$ полученная СЛАУ оказывается плохо обусловленной. Строки матрицы $\mathbf{D} = {\mathbf{A}}^*{\mathbf{BA}}$ могут оказаться почти линейно зависимыми. Простейшим примером такого почти линейно зависимого базиса является система функций xⁱ, i = 1, ..., p при больших p. В этом случае желательно использовать ортогональные функциональные базисы, однако такой выбор не всегда возможен и удобен.

Для примера возьмем в качестве базисных функций степенные, обобщенный полином в этом случае будет

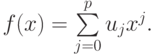
$f(x) = \sum\limits_{j = 0}^p {u_j x^j}.$

Скалярные произведения на отрезке [0, 1], записанные в интегральной форме (т.е. при $n \to \infty$ ), будут иметь вид

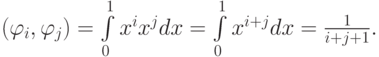
$(\varphi_i,\varphi_j) = \int\limits_0^1 x^i x^j dx = \int\limits_0^1 x^{i + j}dx = \frac{1}{i + j + 1}.$

В таком случае СЛАУ после применения МНК, т.е. минимизации функционала 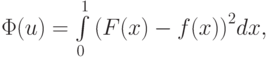$\Phi (u) = \int\limits_0^1 {(F(x) - f(x))}^2dx,$ где F(x) — заданная функция, будет:

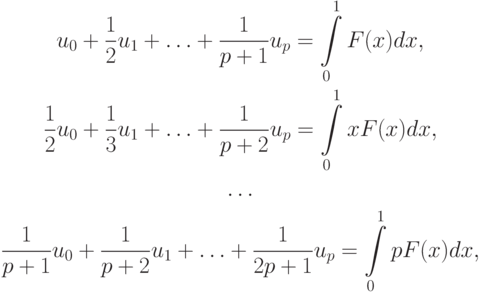
$\begin{gather*} u_0 + \frac{1}{2}u_1 + \ldots + \frac{1}{p + 1}u_p = \int\limits_0^1{F(x)dx}, \\ \frac{1}{2}u_0 + \frac{1}{3}u_1 + \ldots + \frac{1}{p + 2}u_p = \int\limits_0^1 xF(x)dx, \\ \ldots \\ \frac{1}{p + 1}u_0 + \frac{1}{p + 2}u_1 + \ldots + \frac{1}{2p + 1}u_p = \int\limits_0^1 pF(x)dx, \end{gather*}$

или

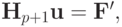
${\mathbf{H}}_{p + 1}\mathbf{u} = \mathbf{F^{\prime}},$

где

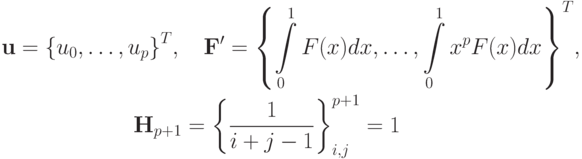
$\begin{gather*} \mathbf{u} = {\{u_0, \ldots, u_p \}}^T,\quad \mathbf{F^{\prime}} = {\left\{{\int\limits_0^1 {F(x)dx}, \ldots, \int\limits_0^1 {x^p F(x)dx}} \right\}}^T, \\ {\mathbf{H}}_{p + 1} = {\left\{\frac{1}{i + j - 1}\right\}}^{p + 1}_{i,j} = 1 \end{gather*}$

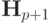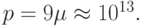Матрица $\mathbf{H}_{p + 1}$ называется матрицей Гильберта. Это классический пример плохо обусловленной матрицы. Число обусловленности очень быстро растет с ростом p. Так при p = 1 $\mu = \left\|\mathbf{H}\right\| \cdot \left\|{\mathbf{H}}^{- 1}\right\| \approx 20,$ при $p = 9 \mu \approx 10^{13}.$ Если получим СЛАУ для дискретной системы точек, т.е. для

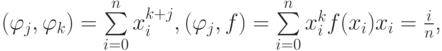
$$ (\varphi_j,\varphi_k) = \sum\limits_{i = 0}^n x^{k + j}_i, (\varphi_j,f) = \sum\limits_{i = 0}^n x^k_i f(x_i)x_i = \frac{i}{n} $,$

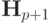то ее матрица будет асимптотически приближаться к матрице Гильберта $\mathbf{H}_{p + 1}$ при $n \rightarrow \infty.$

Дальше >>

Авторизоваться

Введение в вычислительную математику

Численное решение переопределенных СЛАУ. Метод наименьших квадратов

Вопросы и ответы