НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 4: Численное решение переопределенных СЛАУ. Метод наименьших квадратов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3791 / 1086 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 53 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

3.4. Задачи для самостоятельного решения

Задана таблица {x_k, f_k}, k = 0, 1, ..., n, n > 1.
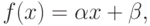Найти линейную функцию $f(x) = \alpha x + \beta,$ минимизирующую функционал $\Phi (\alpha,\beta) = \sum\limits_{k = 0}^n {(f_k - \alpha x_k - \beta)^2} .$

Используя этот результат, решить переопределенную СЛАУ
```
x + y = 3,  x + 3y = 7,  2x - y = 0.2, 3x + y = 5.
```
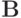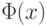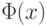Пусть $\mathbf{B}$ — квадратная матрица размером n x n, $\mathbf{u}$ — n -мерный вектор, $\Phi (x)$ — функционал, $\Phi (x) = \left({\mathbf{Bu} - \mathbf{u}x,\mathbf{Bu} - \mathbf{u}x}\right).$ Доказать, что $\Phi (x)$ достигает минимума при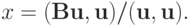 $x = (\mathbf{Bu},\mathbf{u})/(\mathbf{u},\mathbf{u}).$
Барометрическое давление изменяется с высотой по закону p = ae^bh.
Определить коэффициенты a, b по результатам наблюдений, приведенных в таблице ( h — высота в метрах над уровнем моря; p — давление в мм рт. ст.):

h 0 270 840 1452 2116 3203

p 760 737 686 636 584 508
Скорость корабля связана с мощностью его двигателя формулой P = a₀ + a₃v³ ( P — мощность в лошадиных силах, v — скорость в узлах).
Определить a₀, a₃ по табличным данным.

v 6 8 10 12 13

P 423 805 1378 2357 2893
Найти приближение многочленом третьей степени методом наименьших квадратов для функции $f(x) = \sin (\pi x)$ по значениям в точках x₀ = - 1, x₁ = - 0,5, x₂ = 0, x₄ = 1.
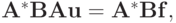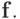
Вычислить матрицы $\mathbf{A^*BA}$ и $\mathbf{A^*B}$ и найти решение системы уравнений вида $\mathbf{A^*BAu} = \mathbf{A^*Bf},$ если заданы матрицы $\mathbf{A}, \mathbf{B}$ и вектор $\mathbf{f}.$
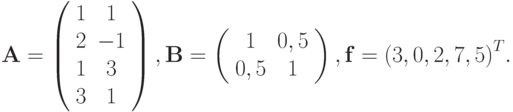
$\mathbf{A} = \left( \begin{array}{cc} 1 & 1 \\ 2 & {- 1} \\ 1 & 3 \\ 3 & 1 \end{array} \right), \mathbf{B} = \left( \begin{array}{cc} 1 & {0,5} \\ {0,5} & 1 \end{array} \right), \mathbf{f} = {(3, 0,2, 7, 5)}^T.$
Функция $f(x) = \sqrt{1 + {\sin}^2 (x - 1)}$ приближенно заменяется тригонометрическим многочленом P(x) = a₀ + a₁sin x + b₁cos x + a₂sin 2x + b₂cos 2x по десяти точкам x₀, ..., x₉ с помощью метода наименьших квадратов.
Опишите алгоритм вычисления коэффициентов a₀, a₁, b₁, a₂, b₂.
Доказать, что прямая, проведенная по методу наименьших квадратов, проходит через точку с координатами
$$ {x^{\prime}} = \frac{\sum\limits_i {y_ix_i}}{\sum\limits_i {y_i}}, y^{\prime} = \frac{\sum\limits_i {x_iy_i}}{\sum\limits_i {x_i}} $.$