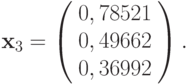Введение в вычислительную математику
[+]
Московский физико-технический институт
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3921 / 1202 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00
ISBN: 978-5-9556-0065-9
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Программист, Математик
Теги: beta, алгебра, алгоритмы, арифметика, вычисления, дифференциальные уравнения, курсы, линейная алгебра, матрица Якоби, метод трапеций, метод Эйлера, норма вектора, поиск, программирование, разделенные разности, разложение в ряд, системы нелинейных уравнений, спектральные задачи, таблицы бутчера, численное решение уравнений, элементы
Лекция 6:

Численное решение нелинейных алгебраических уравнений и систем
A
|
версия для печати
< Лекция 5 || Лекция 6: 12345678910 || Лекция 7 >

5.6. Задачи

  1. Методами простых итераций и Ньютона решить уравнение

    x^2 - e^{- x} = 0, x_0 \in \left[{0.5, 1}\right].

    Решение. Метод простых итераций будет

    $ x_{k + 1} = e^{- \frac{x_k}{2}}, x_0 = 0, 75 $,
    $ F(x) = e^{- \frac{x_k}{2}}, \left|{F^{\prime}_x (x)}\right| < 1 $
    при x \in \left[{0.5, 1}\right].

    Приведем таблицу приближений до точности | x5 - x4 | < 10 - 4.

    k 0 1 2 3 4 5
    xk 0, 75 0, 6873 0, 7091 0, 7015 0, 7042 0, 7032

    Метод Ньютона запишется как

    $ x_{k + 1} = x_k - \frac{{(x_k)}^2 - e^{- x_k}}{2x_k - e^{- x_k}}, x_0 = 1. $

    Результаты расчетов:

    k 0 1 2 3
    xk 1 0, 7330 0, 7038 0, 7035
  2. Построить итерационные методы для вычисления корней уравнения
    x3 + 3x2 - 1 = 0.

    Использовать метод простых итераций.

    Решение. Все три корня данного уравнения лежат на отрезках [- 3, - 2], [- 1, 0], [0, 1].

    Построим итерационный процесс для вычисления первого корня, лежащего на отрезке [- 3, - 2]:

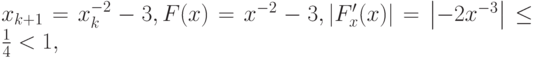
    $ x_{k + 1} = x_k ^{- 2} - 3, F(x) = x^{- 2} - 3, \left|{F^{\prime}_x (x)}\right| = \left|{- 2x^{- 3}}\right| \le \frac{1}{4} < 1, $

    т.е. для начального приближения x_0 \in \left[{- 3, - 2}\right] метод простых итераций сходится.

    Для вычисления двух оставшихся корней, лежащих на отрезках [- 1, 0] и [0, 1], построим итерационный метод

    x_{k + 1} = \pm (x_k + 3)^{- \frac{1}{2}}, F(x) = \pm (x_k + 3)^{- \frac{1}{2}}. $

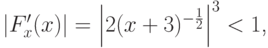    Поскольку для рассматриваемых отрезков {\left|{F^{\prime}_x (x)}\right| = \left|{2(x + 3)^{- \frac{1}{2}}}\right|^3 < 1} $, то этот итерационный процесс сходится к корням рассматриваемого уравнения.

  3. Исследовать сходимость итерационного метода релаксации для численного решения уравнения вида f(x) = 0:
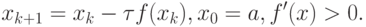
    x_{k + 1} = x_{k} - \tau f(x_{k}), x_{0} = a, f'(x) > 0.

    Решение. Итерационный метод релаксации записывается как

    xk + 1 = F(xk), x0 = 0,

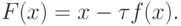
    F(x) = x - \tau f(x).

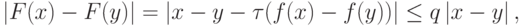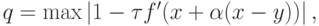
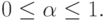
    Из условия того, что отображение является сжимающим, получим \left|{F(x) - F(y)}\right| = \left|{x - y - \tau (f(x) - f(y))}\right| \le q\left|{x - y}\right|, где q = \max \left|{1 - \tau f^{\prime}(x + \alpha (x - y))}\right|, 0 \le \alpha \le 1.

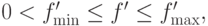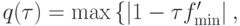
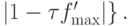
    Положим 0 < f^{\prime}_{\min } \le f^{\prime} \le f^{\prime}_{\max }, тогда {q}(\tau ) = \max \left\{\left|{1 - \tau f^{\prime}_{\min }}\right|\right., \left.\left|{1 - \tau f^{\prime}_{\max}}\right|\right\}.

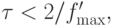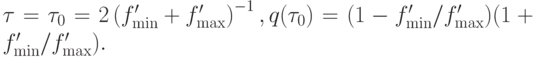
    Отсюда видно, что итерационный процесс будет сходиться, если \left|{1 - \tau f^{\prime}_{\max }}\right| < 1, или \tau < 2/f^{\prime}_{\max } , а оптимальное значение параметра, при котором q = qmin достигается при \left|{1 - \tau f^{\prime}_{\min }}\right| = \left|{1 - \tau f^{\prime}_{\max }}\right|, или \tau = \tau_0 = 2\left({f^{\prime}_{\min } + f^{\prime}_{\max }}\right)^{- 1}, q(\tau_0) = (1 - f^{\prime}_{\min } /f^{\prime}_{\max })(1 + f^{\prime}_{\min } /f^{\prime}_{\max }).

  4. Построить метод простых итераций и итерационный процесс Ньютона для системы уравнений
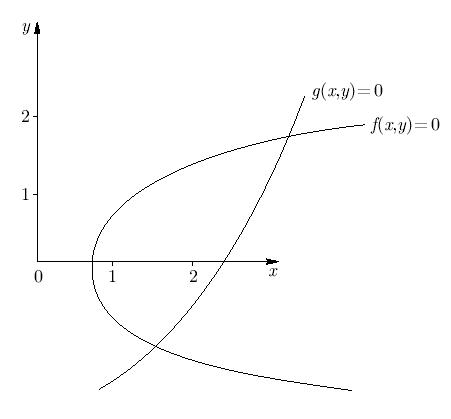
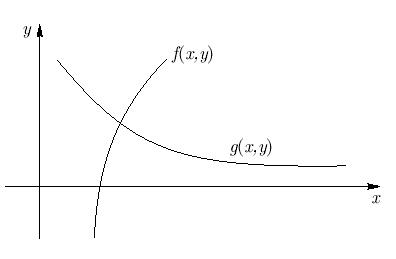
    f(x, y) = x + 3 lg x - y2 = 0, 
 g(x, y) = 2x2 - xy - 5x + 1 = 0.

    Решение. Графики функций f(x, y) и g(x, y) приведены на рис. 5.12.


    Рис. 5.12.

    Метод простых итераций запишем как

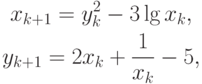
    \begin{gather*} x_{k + 1} = y_k ^2 - 3\lg x_k, \\ y_{k + 1} = 2x_k + \frac{1}{x_k} - 5, \end{gather*}

    где

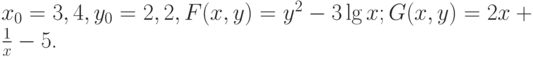
    $ x_0 = 3, 4, y_0 = 2, 2, F(x, y) = y^2 - 3 \lg x; G(x, y) = 2x + \frac{1}{x} - 5 $.

    Матрица Якоби для такого процесса запишется как

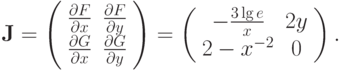
    $ {\mathbf{J}} = \left( \begin{array}{cc} {\frac{\partial F}{\partial x}} & {\frac{\partial F}{\partial y}} \\ {\frac{\partial G}{\partial x}} & {\frac{\partial G}{\partial y}} \\ \end{array} \right) = \left( \begin{array}{cc} {- \frac{3\lg e}{x}} & {2y} \\ {2 - x^{- 2}} & 0 \\ \end{array} \right). $

    Несложно проверить, вычислив норму матрицы Якоби, что для приведенного начального приближения достаточное условие сходимости не выполняется.

    Рассмотрим другой итерационный процесс:

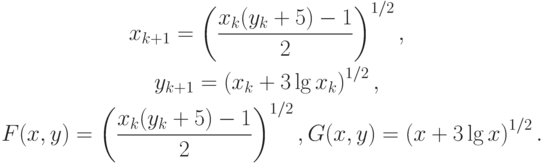
    \begin{gather*} x_{k + 1} = \left({\frac{x_k (y_k + 5) - 1}{2}}\right)^{1/2}, \\ y_{k + 1} = \left({x_k + 3\lg x_k}\right)^{1/2}, \\ F(x, y) = \left({\frac{x_k (y_k + 5) - 1}{2}}\right)^{1/2}, G(x, y) = \left({x + 3\lg x}\right)^{1/2}. \end{gather*}

    Матрица Якоби для этого итерационного метода будет

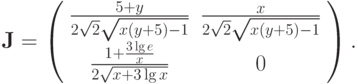
    $ {\mathbf{J}} = \left( \begin{array}{cc} {\frac{5 + y}{2\sqrt{2} \sqrt{x(y + 5) - 1}}} & {\frac{x}{{2\sqrt{2} \sqrt {x(y + 5) - 1}}}} \\ {\frac{{1 + \frac{{3\lg e}}{x}}}{{2\sqrt {x + 3\lg x}}}} & 0 \\ \end{array} \right). $

    В окрестности начального приближения условие сходимости выполнено. Таблица первых пяти приближений будет

    k 0 1 2 3 4 5
    x 3, 4 3, 426 3, 451 3, 466 3, 475 3, 480
    y 2, 2 2, 243 2, 2505 2, 255 2, 258 2, 259
  5. Построить итерационный метод Ньютона для вычисления \sqrt[n]{a}, a > 0, n \in R.

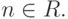
    Решение. Найдем корень уравнения

    f(x) = xn - a = 0.

    Метод Ньютона для этого уравнения запишется

    \begin{gather*} x_{k + 1} = x_k - \frac{{f\left({x_k}\right)}}{{f^{\prime}\left({x_k}\right)}} = x_k - \frac{{x_n^{k} - a}}{{nx_m^{p - 1}}} = \\ = \frac{{n - 1}}{n}x_k + \frac{a}{{nx_k^{n - 1}}} = \frac{1}{n}\left[{\left({n - 1}\right)x_k + \frac{a}{{x_k^{n - 1}}}}\right]. \end{gather*}

    В частности, при n = 2 имеем

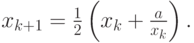
    $ x_{k + 1} = \frac{1}{2}\left({x_k + \frac{a}{x_k}}\right). $
  6. Получить расчетные формулы метода Ньютона для численного решения системы двух нелинейных уравнений f(x, y) = 0, g(x, y) = 0.

    Решение. Положим 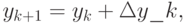x_{k + 1} = \Delta x_{k}, y_{k + 1} = y_{k} + \Delta y\_ k, f(xk, yk) = fk, получим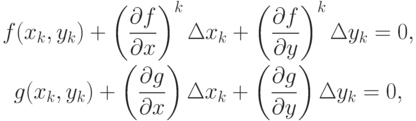

    \begin{gather*} f(x_k , y_k) + \left({\frac{\partial f}{\partial x}}\right)^{k} \Delta x_k + \left({\frac{\partial f}{\partial y}}\right)^{k} \Delta y_k = 0, \\ g(x_k , y_k) + \left({\frac{\partial g}{\partial x}}\right)\Delta x_k + \left({\frac{\partial g}{\partial y}}\right)\Delta y_k = 0, \end{gather*}

    откуда

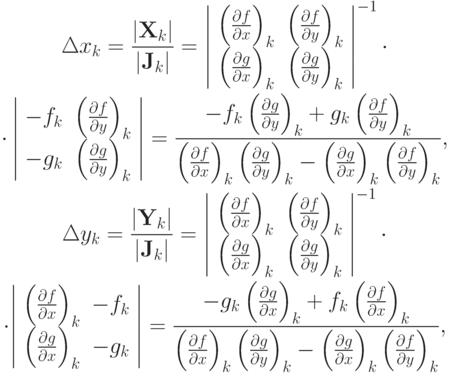
    \begin{gather*} \Delta x_k = \frac{{\left|{{\mathbf{X}}_k}\right|}}{{\left|{{\mathbf{J}}_k}\right|}} = \left| \begin{array}{cc} {\left({\frac{{\partial f}} {{\partial x}}}\right)_k} & {\left({\frac{{\partial f}} {{\partial y}}}\right)_k} \\ {\left({\frac{{\partial g}} {{\partial x}}}\right)_k} & {\left({\frac{{\partial g}} {{\partial y}}}\right)_k} \\ \end{array} \right|^{- 1}\cdot \\ \cdot \left| \begin{array}{cc} {- f_k} & {\left({\frac{\partial f}{\partial y}}\right)_k} \\ {- g_k} & {\left({\frac{\partial g}{\partial y}}\right)_k} \\ \end{array} \right| = \frac{{- f_k \left({\frac{\partial g}{\partial y}}\right)_k + g_k \left({\frac{\partial f}{\partial y}}\right)_k}} {{\left({\frac{\partial f}{\partial x}}\right)_k \left({\frac{\partial g}{\partial y}}\right)_k - \left({\frac{\partial g}{\partial x}}\right)_k \left({\frac{\partial f}{\partial y}}\right)_k}}, \\ \Delta y_k = \frac{{\left|{{\mathbf{Y}}_k}\right|}} {{\left|{{\mathbf{J}}_k}\right|}} = \left| \begin{array}{cc} {\left({\frac{{\partial f}} {{\partial x}}}\right)_k} & {\left({\frac{{\partial f}} {{\partial y}}}\right)_k} \\ {\left({\frac{{\partial g}} {{\partial x}}}\right)_k} & {\left({\frac{{\partial g}} {{\partial y}}}\right)_k} \\ \end{array} \right|^{- 1} \cdot \\ \cdot {\left| \begin{array}{cc} {\left({\frac{{\partial f}} {{\partial x}}}\right)_k} & {- f_k} \\ {\left({\frac{{\partial g}} {{\partial x}}}\right)_k} & {- g_k} \\ \end{array} \right|} = \frac{{- g_k \left({\frac{{\partial g}} {{\partial x}}}\right)_k + f_k \left({\frac{{\partial f}} {{\partial x}}}\right)_k}} {{\left({\frac{{\partial f}} {{\partial x}}}\right)_k \left({\frac{{\partial g}} {{\partial y}}}\right)_k - \left({\frac{{\partial g}} {{\partial x}}}\right)_k \left({\frac{{\partial f}} {{\partial y}}}\right)_k}}, \end{gather*}

    где

    $ \mathbf{J}_k = \left( \begin{array}{cc} {\left({\frac{{\partial f}} {{\partial x}}}\right)_k} & {\left({\frac{{\partial f}} {{\partial y}}}\right)_k} \\ {\left({\frac{{\partial g}} {{\partial x}}}\right)_k} & {\left({\frac{{\partial g}} {{\partial y}}}\right)_k} \\ \end{array} \right) $
    — матрица Якоби,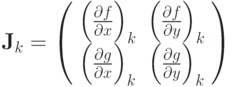 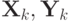{\mathbf{X}}_k , {\mathbf{Y}}_k — матрицы

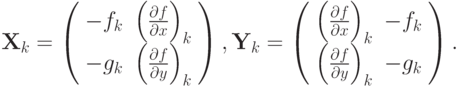
    $ {\mathbf{X}}_k = \left( \begin{array}{cc} {- f_k} & {\left({\frac{{\partial f}} {{\partial x}}}\right)_k} \\ {- g_k} & {\left({\frac{{\partial f}} {{\partial y}}}\right)_k} \\ \end{array} \right), {\mathbf{Y}}_k = \left( \begin{array}{cc} {\left({\frac{{\partial f}} {{\partial x}}}\right)_k} & {- f_k} \\ {\left({\frac{{\partial f}} {{\partial y}}}\right)_k} & {- g_k} \\ \end{array} \right). $

    Тогда запишем расчетные формулы для итерационного метода Ньютона:

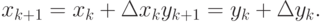
    x_{k + 1} = x_{k} + \Delta x_{k} y_{k + 1} = y_{k} + \Delta y_{k}.
  7. Найти приближенное решение системы двух нелинейных алгебраических уравнений x3 - y3 - 1 = 0, xy3 - y - 4 = 0, используя метод Ньютона.

    Решение.

    Пусть f(x, y) = x3 - y3 - 1, g(x, y) = xy3 - y - 4. Начальное приближение можно найти графически: x0 = y0 = 1, 5.


    Матрицы 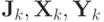\mathbf{J}_k, \mathbf{X}_k, \mathbf{Y}_k в этом случае будут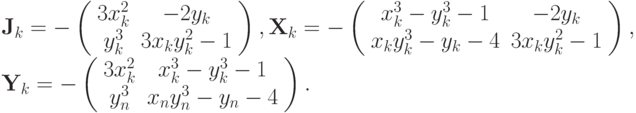

    {\mathbf{J}}_k = - \left( \begin{array}{cc} {3x_k^2} & {- 2y_k} \\ {y_k^3} & {3x_k y_k^2 - 1} \\ \end{array} \right), {\mathbf{X}}_k = - \left( \begin{array}{cc} {x_k^3 - y_k^3 - 1} & {- 2y_k} \\ {x_k y_k^3 - y_k - 4} & {3x_k y_k^2 - 1} \\ \end{array} \right), \\ {\mathbf{Y}}_k = - \left( \begin{array}{cc} {3x_k^2} & {x_k^3 - y_k^3 - 1} \\ {y_n^3} & {x_n y_n^3 - y_n - 4} \\ \end{array} \right).

    Следующее приближение вычисляется по формуле Ньютона:

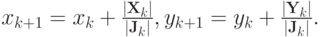
    $ x_{k + 1} = x_k + \frac{{\left|{{\mathbf{X}}_k}\right|}} {{\left|{{\mathbf{J}}_k}\right|}}, y_{k + 1} = y_k + \frac{{\left|{{\mathbf{Y}}_k}\right|}} {{\left|{{\mathbf{J}}_k}\right|}}. $

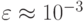    Результаты вычислений первых двух итераций приведены в таблице (точность \varepsilon \approx 10^{ - 3} ) .

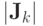
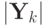
    k xk; yk fk; gk {\left|\mathbf{J}_k\right|} {\left|\mathbf{X}_k\right|} {\left|\mathbf{Y}_k\right|}
    0 1,5;

    1,5;

    		 0,12500

    -4,33750

    		 71,71875 -0,171875 -3,3750
    1 1,502397

    1,547059

    		 -0,002170

    0,015844

    		 77,73277 0,0277988 0,1153255
    2 1,5020396

    1,545570

    		 0,0000017

    0,000019

    Найти приближенное решение системы трех нелинейных уравнений x2 + y2 + z2 = 1, 2x2 + y2 - 4z = 0, 3x2 - 4y + z2 = 0, используя метод Ньютона. За начальное приближение решения выбрать точку x0 = y0 = z0 = 0, 5.

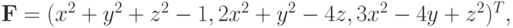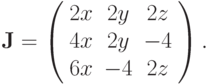    Решение. Обозначим {\mathbf{F}} = (x^2 + y^2 + z^2 - 1, 2x^2 + y^2 - 4z, 3x^2 - 4y + z^2 )^T , тогда матрица Якоби будет {\mathbf{J}} = \left( \begin{array}{ccc} {2x} & {2y} & {2z} \\ {4x} & {2y} & {- 4} \\ {6x} & {- 4} & {2z} \end{array} \right). Соответственно, для точки начального приближения вычислим

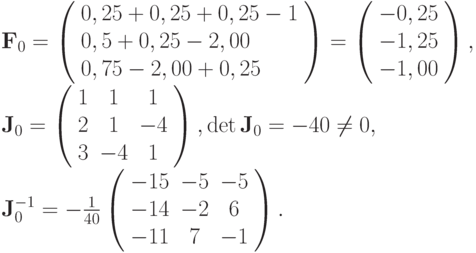
    $ {\mathbf{F}}_0 = \left( \begin{array}{l} 0, 25 + 0, 25 + 0, 25 - 1 \\ 0, 5 + 0, 25 - 2, 00 \\ 0, 75 - 2, 00 + 0, 25 \end{array} \right) = \left( \begin{array}{l} - 0, 25 \\ - 1, 25 \\ - 1, 00 \\ \end{array} \right), \\ {\mathbf{J}}_0 = \left( \begin{array}{ccc} 1 & 1 & 1 \\ 2 & 1 & {- 4} \\ 3 & {- 4} & 1 \\ \end{array} \right), \det {\mathbf{J}}_0 = - 40 \ne 0, \\ {\mathbf{J}}_0^{ - 1} = - \frac{1} {{40}}\left( \begin{array}{ccc} {- 15} & {- 5} & {- 5} \\ {- 14} & {- 2} & 6 \\ {- 11} & 7 & {- 1} \\ \end{array} \right). $

    Вычислим первое приближение

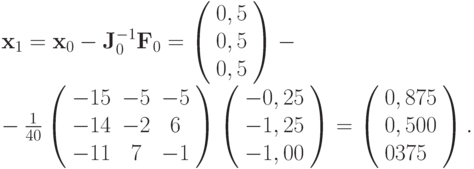
    $ {\mathbf{x}}_1 = {\mathbf{x}}_0 - {\mathbf{J}}_0^{- 1}{\mathbf{F}}_0 = \left( \begin{array}{l} 0, 5 \\ 0, 5 \\ 0, 5 \\ \end{array} \right) - \\ - \frac{1} {{40}}\left( \begin{array}{ccc} {- 15} & {- 5} & {- 5} \\ {- 14} & {- 2} & 6 \\ {- 11} & 7 & {- 1} \\ \end{array} \right) \left( \begin{array}{l} - 0, 25 \\ - 1, 25 \\ - 1, 00 \\ \end{array} \right) = \left( \begin{array}{l} 0, 875 \\ 0, 500 \\ 0375 \\ \end{array} \right). $

    Для второго приближения

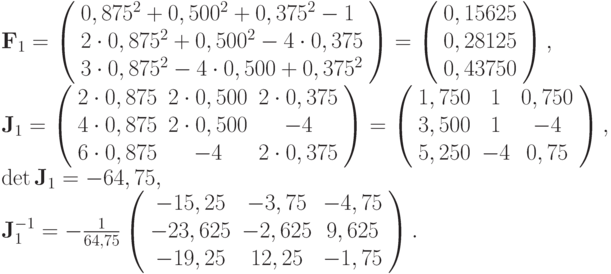
    $ {\mathbf{F}}_1 = \left( \begin{array}{l} 0, 875^2 + 0, 500^2 + 0, 375^2 - 1 \\ 2 \cdot 0, 875^2 + 0, 500^2 - 4 \cdot 0, 375 \\ 3 \cdot 0, 875^2 - 4 \cdot 0, 500 + 0, 375^2 \\ \end{array} \right) = \left( \begin{array}{l} 0, 15625 \\ 0, 28125 \\ 0, 43750 \\ \end{array} \right), \\ {\mathbf{J}}_1 = \left( \begin{array}{ccc} {2 \cdot 0, 875} & {2 \cdot 0, 500} & {2 \cdot 0, 375} \\ {4 \cdot 0, 875} & {2 \cdot 0, 500} & {- 4} \\ {6 \cdot 0, 875} & {- 4} & {2 \cdot 0, 375} \\ \end{array} \right) = \left( \begin{array}{ccc} {1, 750} & 1 & {0, 750} \\ {3, 500} & 1 & {- 4} \\ {5, 250} & {- 4} & {0, 75} \\ \end{array} \right), \\ \det {\mathbf{J}}_1 = - 64, 75, \\{\mathbf{J}}_1^{- 1} = - \frac{1} {{64, 75}}\left( \begin{array}{ccc} {- 15, 25} & {- 3, 75} & {- 4, 75} \\ {- 23, 625} & {- 2, 625} & {9, 625} \\ {- 19, 25} & {12, 25} & {- 1, 75} \\ \end{array} \right). $

    По формуле Ньютона получим

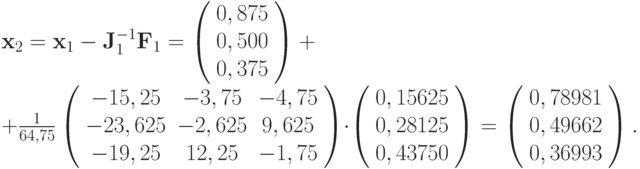
    $ {\mathbf{x}}_2 = {\mathbf{x}}_1 - {\mathbf{J}}_1^{- 1} {\mathbf{F}}_1 = \left( \begin{array}{l} 0, 875 \\ 0, 500 \\ 0, 375 \\ \end{array} \right) + \\ + \frac{1} {{64, 75}}\left( \begin{array}{ccc} {- 15, 25} & {- 3, 75} & {- 4, 75} \\ {- 23, 625} & {- 2, 625} & {9, 625} \\ {- 19, 25} & {12, 25} & {- 1, 75} \\ \end{array} \right) \cdot \left( \begin{array}{l} 0, 15625 \\ 0, 28125 \\ 0, 43750 \\ \end{array} \right) = \left( \begin{array}{l} 0, 78981 \\ 0, 49662 \\ 0, 36993 \\ \end{array} \right). $

    Аналогично находим третье приближение, которым и ограничимся:

    {\mathbf{x}}_3 = \left( \begin{array}{l} 0, 78521 \\ 0, 49662 \\ 0, 36992 \\ \end{array} \right).
Дальше >>
< Лекция 5 || Лекция 6: 12345678910 || Лекция 7 >

Вопросы и ответы

вопросов: 1
Sanjar Ibrohimov
Sanjar Ibrohimov
ответить