Введение в вычислительную математику
[+]
Московский физико-технический институт
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3921 / 1202 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00
ISBN: 978-5-9556-0065-9
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Программист, Математик
Теги: beta, алгебра, алгоритмы, арифметика, вычисления, дифференциальные уравнения, курсы, линейная алгебра, матрица Якоби, метод трапеций, метод Эйлера, норма вектора, поиск, программирование, разделенные разности, разложение в ряд, системы нелинейных уравнений, спектральные задачи, таблицы бутчера, численное решение уравнений, элементы
Лекция 6:

Численное решение нелинейных алгебраических уравнений и систем
A
|
версия для печати
< Лекция 5 || Лекция 6: 12345678910 || Лекция 7 >

5.7. Задачи для самостоятельного решения

  1. Исследовать возможность применения трех итерационных процессов

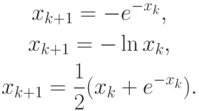
    \begin{gather*} x_{k + 1} = - e^{- x_k}, \\ x_{k + 1} = - \ln x_k, \\ x_{k + 1} = \frac{1}{2}(x_k + e^{- x_k}). \end{gather*}

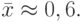
    для численного решения уравнения x + ln x = 0, имеющего корень \bar {x} \approx 0, 6.

  2. Исследовать сходимость процесса простой итерации в зависимости от начального приближения для численного решения уравнения
    x - 2x - 1 = 0,

    имеющего корни x1 = 1, x2 = 2.

  3. Предложить процессы простых итераций для решения уравнений

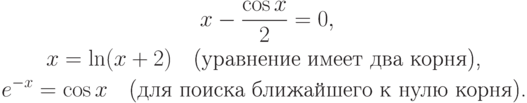
    \begin{gather*} x - \frac{\cos x}{2} = 0, \\ x = \ln (x + 2)\quad \mbox{(уравнение имеет два корня), } \\ e^{- x} = \cos x \quad \mbox{(для поиска ближайшего к нулю корня). } \end{gather*}

  4. Предложить итерационный процесс Ньютона для вычисления решений систем уравнений

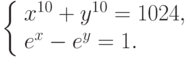
    \left\{ \begin{array}{l} {x^{10} + y^{10} = 1024, } \\ {e^{x} - e^{y} = 1.} \\ \end{array} \right.

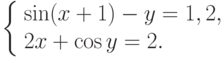
    \left\{ \begin{array}{l} {\sin (x + 1) - y = 1, 2, } \\ {2x + \cos y = 2.} \\ \end{array} \right.

  5. Предложить методы простых итераций и Ньютона для численного решения нелинейных уравнений:

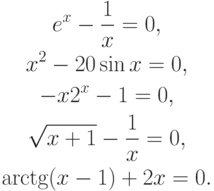
    \begin{gather*} e^{x} - \frac{1}{x} = 0, \\ x^2 - 20\sin x = 0, \\ - x 2^{x} - 1 = 0, \\ \sqrt{x + 1} - \frac{1}{x} = 0, \\ \arctg (x - 1) + 2x = 0. \end{gather*}

  6. С помощью методов дихотомии и Ньютона найти точку локального минимума функции 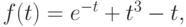f(t) = e^{- t} + t^3 - t, с точностью \varepsilon = 10^{- 6}.$
Дальше >>
< Лекция 5 || Лекция 6: 12345678910 || Лекция 7 >

Вопросы и ответы

вопросов: 1
Sanjar Ibrohimov
Sanjar Ibrohimov
ответить