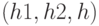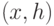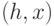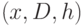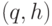|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Объединяемые приоритетные очереди
Наконец, сливаем кучи  и
и 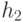 , получая в
результате левостороннюю кучу (рис. 5.19).
, получая в
результате левостороннюю кучу (рис. 5.19).
Реализация операции УМЕНЬШИТЬ_КЛЮЧ
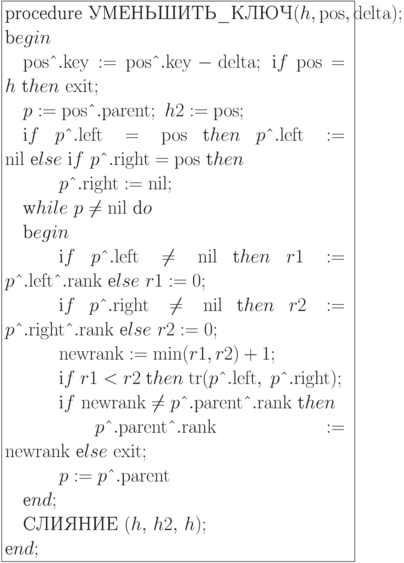
Операция ОБРАЗОВАТЬ_ОЧЕРЕДЬ.
Из элементов списка 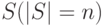 образуется
левосторонняя куча
образуется
левосторонняя куча  . Способ формирования такой кучи
посредством
. Способ формирования такой кучи
посредством  применений операции ВСТАВИТЬ неэффективен.
Читателю предоставляется возможность доказать, что в худшем случае
формирование кучи таким способом может потребовать
применений операции ВСТАВИТЬ неэффективен.
Читателю предоставляется возможность доказать, что в худшем случае
формирование кучи таким способом может потребовать 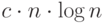 операций, где
операций, где  .
.
Более эффективным является следующий способ образования  -элементной левосторонней кучи. Заводится список
-элементной левосторонней кучи. Заводится список  , в который
помещаются
, в который
помещаются  одноэлементных куч. Пока длина списка
одноэлементных куч. Пока длина списка  больше 1, из его начала
извлекаются две кучи, производится их слияние, а полученная куча
вставляется в конец списка
больше 1, из его начала
извлекаются две кучи, производится их слияние, а полученная куча
вставляется в конец списка  .
.
Читателю предоставляется возможность доказать, что время выполнения
операции ОБРАЗОВАТЬ_ОЧЕРЕДЬ таким способом —  .
.
Реализация операции ОБРАЗОВАТЬ_ОЧЕРЕДЬ