|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Машины Тьюринга
Исторические сведения
К концу XIX - началу XX века в математике накопилось некоторое количество вычислительных задач, для которых ученые, несмотря на упорные попытки, не могли предложить методов решения. Одной из таких задач является задача о разрешимости диофантова уравнения. В докладе Д.Гильберта, прочитанном на II Международном конгрессе математиков в августе 1900 года, она звучит следующим образом:
"Пусть задано диофантово уравнение с произвольными неизвестными и целыми рациональными числовыми коэффициентами. Указать способ, при помощи которого возможно после конечного числа операций установить, разрешимо ли это уравнение в целых рациональных числах".
Неудачные попытки математиков решить эту и другие подобные задачи привели к мысли о том, что метода их решения может и не существовать. Но, чтобы доказывать подобного рода утверждения, необходимо иметь математическое определение метода, то есть для интуитивных понятий разрешимости и вычислимости необходимо иметь их формальные эквиваленты. Одним из важнейших достижений математики XX века является формирование математических понятий, которые раскрывают сущность интуитивных представлений о том, что такое метод (алгоритм) решения той или иной задачи, что такое вычислимая функция.
Важность этих понятий вытекает не только из общенаучных проблем развития математики, но также из практических задач общества, использующего вычислительную технику в производстве, экономике, инженерных расчетах и нуждающегося в адекватном представлении о возможностях вычислительных автоматов. Приведем краткие исторические сведения о возникновении теории алгоритмов.
В 1932-1935 годах А.Черч и С.К.Клини ввели понятие 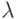 -определимой
функции, которое сыграло важную роль в определении объема интуитивного
понятия вычислимой функции.
-определимой
функции, которое сыграло важную роль в определении объема интуитивного
понятия вычислимой функции.
В 1934 году К.Гедель, на основе идей Дж.Эрбрана, рассмотрел класс
функций, названных общерекурсивными, а в 1936 году А.Черч и С.К.Клини
доказали, что этот класс совпадает с классом 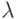 -определимых
функций.
-определимых
функций.
В 1936 году А.Тьюринг ввел свое понятие вычислимой функции, а в 1937 году
доказал, что оно совпадает с понятием 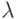 -определимой функции.
-определимой функции.
В 1943 году Э.Пост, основываясь на своей неопубликованной работе 1920-1922 годов, выдвинул еще один формальный эквивалент понятия вычислимой функции.
Еще одну формулировку дает теория алгоритмов Маркова (1951 г.).
Любое из упомянутых здесь уточнений интуитивного понятия вычислимой функции можно принять за математическое определение класса вычислимых функций. Основными доводами для этого являются эквивалентность различных формулировок и естественно-исторический опыт, показывающий, что все изучавшиеся до сих пор функции, которые принято считать вычислимыми, являются таковыми в смысле любого из упомянутых выше определений.
Еще один подход к моделированию вычислений развивается в рамках так называемого логического программирования. При таком подходе условия решаемой задачи и ее цель формулируются с помощью предложений формального логического языка. Затем осуществляется автоматический поиск доказательства цели, сопровождаемый вычислением неизвестных в задаче величин.
Заметим, что разрабатываемые в настоящее время алгоритмические языки,
составляющие математическое обеспечение современных вычислительных
устройств, также можно использовать для определения понятия вычислимости.
Более того, можно проследить тесную связь между упомянутыми здесь
теоретическими моделями вычислений и реальным программированием.
Так, 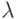 -исчисление Черча является прообразом функционального
программирования, реализованного в известном программистам языке ЛИСП, разработанном
в 1961 году Дж.Маккарти, а модель Поста содержит идеи, реализованные
в операторных языках типа Фортран, Алгол. Методы логического
программирования реализованы в настоящее время в нескольких версиях языка Пролог.
-исчисление Черча является прообразом функционального
программирования, реализованного в известном программистам языке ЛИСП, разработанном
в 1961 году Дж.Маккарти, а модель Поста содержит идеи, реализованные
в операторных языках типа Фортран, Алгол. Методы логического
программирования реализованы в настоящее время в нескольких версиях языка Пролог.
Однако реальные языки программирования из-за своей громоздкости и избыточности выразительных средств малопригодны для теоретического анализа понятия вычислимости. Отметим также модели вычислительных устройств, получившие название РАМ (Равнодоступная Адресная Машина) и РАСП (Равнодоступная Адресная Машина С хранимой Программой). Эти модели в большей степени, чем, например, модель Тьюринга, отражают структуру современных вычислительных устройств.
