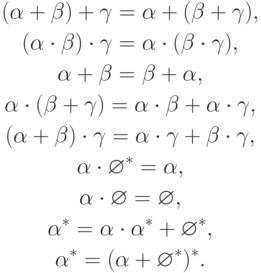|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Формальные языки
Основные понятия и обозначения
Алфавит — конечное множество абстрактных символов, как правило, упорядоченное в так называемом алфавитном порядке.
Слово (в алфавите  ) —
конечная последовательность символов (алфавита).
) —
конечная последовательность символов (алфавита).
Длина
слова — количество вхождений
символов в слово. Длина слова  , обычно обозначается
, обычно обозначается  .
.
Пустое слово — пустая последовательность, то есть
последовательность, не содержащая ни одного символа. Пустое слово,
соблюдая традиции, часто обозначают греческой буквой 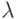 , полагая
при этом, что она не является символом рассматриваемого алфавита.
, полагая
при этом, что она не является символом рассматриваемого алфавита.
Слово длины  (
(  ) можно отождествить
с элементом декартова произведения (
) можно отождествить
с элементом декартова произведения ( 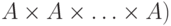 ,
в котором
,
в котором  сомножителей, обозначаемого
сомножителей, обозначаемого 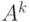 . При
. При 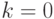 имеем
имеем 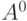 , состоящее из одного пустого слова; не путать с пустым
множеством, обозначаемым знаком
, состоящее из одного пустого слова; не путать с пустым
множеством, обозначаемым знаком  .
.
Замечание. При отождествлении элемента декартова произведения со словом полагаем, что слово составлено из входящих в него символов в соответствующем порядке.
Множество всех слов в алфавите  обозначают
обозначают

Множество всех непустых слов в алфавите  обозначают
обозначают
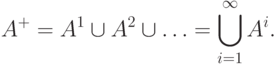
Сверхслово (в алфавите  )
— бесконечная последовательность символов (алфавита
)
— бесконечная последовательность символов (алфавита  ).
).
Формальный язык (в алфавите  ) — множество слов
(в алфавите
) — множество слов
(в алфавите  ).
).
Конкатенация слов — двухместная операция над словами,
заключающаяся в приписывании второго слова к первому. Результат
конкатенации слов  и
и  обозначается
обозначается  .
.
Начальный фрагмент слова  ,
имеющий длину
,
имеющий длину  , называется префиксом длины
, называется префиксом длины  слова
слова  , обозначается
, обозначается  .
.
Конечный фрагмент слова  , имеющий длину
, имеющий длину  ,
называется суффиксом длины
,
называется суффиксом длины  слова
слова  , обозначается
, обозначается  .
.
Если  , то префикс и суффикс называются
собственными. Заметим, что при нашем определении пустое слово
, то префикс и суффикс называются
собственными. Заметим, что при нашем определении пустое слово 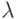 будет и собственным префиксом, и собственным суффиксом любого
слова
будет и собственным префиксом, и собственным суффиксом любого
слова  .
.
Операции над формальными языками. Поскольку формальные языки являются множествами, то к ним применяются обычные теоретико-множественные операции: объединение, пересечение, дополнение (до множества всех слов в рассматриваемом алфавите). Кроме перечисленных, применяются специфические операции — это конкатенация двух языков и итерация языка.
Результатом конкатенации языков 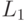 и
и 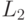 является язык
является язык 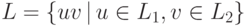 , обозначаемый
также
, обозначаемый
также 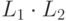 . Результат конкатенации
. Результат конкатенации  экземпляров языка
экземпляров языка  обозначим через
обозначим через 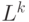 .
.
Результатом итерации языка  является язык
является язык 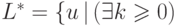
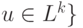 . Заметим, что
. Заметим, что 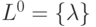 и поэтому
и поэтому 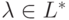 при любом
при любом  .
.
Замечание. При работе с формальными языками операцию
объединения часто обозначают знаком " 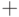 ". В следующих
тождествах используется именно это соглашение.
". В следующих
тождествах используется именно это соглашение.
Основные тождества. Пусть  ,
,  ,
,  — произвольные формальные языки над некоторым фиксированным
алфавитом, тогда справедливы следующие тождества:
— произвольные формальные языки над некоторым фиксированным
алфавитом, тогда справедливы следующие тождества: