|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Разделенные множества
Разделенные множества — это
абстрактный тип данных,
предназначенный для представления коллекции, состоящей из некоторого
числа  попарно непересекающихся подмножеств
попарно непересекающихся подмножеств  заданного множества
заданного множества  . Для простоты в качестве
. Для простоты в качестве  будем рассматривать множество
будем рассматривать множество 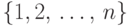 .
.
Этот тип данных применяется в таких задачах, как поиск минимального остовного дерева для заданного взвешенного неориентированного графа, построение компонент связности графа, минимизация конечного автомата, и многих других, требующих динамического поддержания некоторого отношения эквивалентности. Примеры таких задач будут рассмотрены ниже.
Как правило, в таких задачах вычисления начинаются с пустой коллекции
подмножеств (  ). Затем по мере вычислений формируются
новые подмножества, включаемые в коллекцию. Формирование новых подмножеств
происходит либо путем создания одноэлементного подмножества, либо путем
объединения уже существующих в коллекции подмножеств. Для осуществления
таких действий используются имена включенных в коллекцию подмножеств. В
качестве имени подмножества будем использовать один из его элементов
(главный элемент), выбираемый по определенному правилу. Поскольку в
коллекции всегда будут находиться попарно непересекающиеся подмножества
множества
). Затем по мере вычислений формируются
новые подмножества, включаемые в коллекцию. Формирование новых подмножеств
происходит либо путем создания одноэлементного подмножества, либо путем
объединения уже существующих в коллекции подмножеств. Для осуществления
таких действий используются имена включенных в коллекцию подмножеств. В
качестве имени подмножества будем использовать один из его элементов
(главный элемент), выбираемый по определенному правилу. Поскольку в
коллекции всегда будут находиться попарно непересекающиеся подмножества
множества  , такое имя будет однозначно определять требуемое
подмножество.
, такое имя будет однозначно определять требуемое
подмножество.
Операции над разделенными множествами
СОЗДАТЬ (  ). Эта
операция предназначена для введения
в коллекцию нового подмножества, состоящего из одного элемента
). Эта
операция предназначена для введения
в коллекцию нового подмножества, состоящего из одного элемента  ,
при этом предполагается, что
,
при этом предполагается, что  не входит ни в одно из подмножеств
коллекции, созданной к моменту выполнения этой операции.
Элемент
не входит ни в одно из подмножеств
коллекции, созданной к моменту выполнения этой операции.
Элемент  указывается в качестве параметра.
Именем созданного подмножества будет считаться сам элемент
указывается в качестве параметра.
Именем созданного подмножества будет считаться сам элемент  .
.
ОБЪЕДИНИТЬ (  ).
С помощью этой операции можно объединить два подмножества коллекции, имеющие, соответственно,
имена
).
С помощью этой операции можно объединить два подмножества коллекции, имеющие, соответственно,
имена  и
и  , в одно новое подмножество, при этом оба
объединяемые подмножества удаляются из коллекции, а вновь построенное подмножество
получает некоторое имя. Во всех рассматриваемых нами случаях именем нового
полученного в результате этой операции подмножества будет одно из
имен
, в одно новое подмножество, при этом оба
объединяемые подмножества удаляются из коллекции, а вновь построенное подмножество
получает некоторое имя. Во всех рассматриваемых нами случаях именем нового
полученного в результате этой операции подмножества будет одно из
имен  или
или  . Имена объединяемых подмножеств указываются
в качестве параметров.
. Имена объединяемых подмножеств указываются
в качестве параметров.
НАЙТИ (  ). Эта
операция позволяет определить имя
). Эта
операция позволяет определить имя  того подмножества коллекции, которому принадлежит элемент
того подмножества коллекции, которому принадлежит элемент  . Если
элемент
. Если
элемент  до выполнения операции не входил ни в одно из
подмножеств коллекции, то в качестве
до выполнения операции не входил ни в одно из
подмножеств коллекции, то в качестве  берется 0.
берется 0.
Последовательность  , составленную из операций типа
СОЗДАТЬ, ОБЪЕДИНИТЬ, НАЙТИ, назовем корректной, если перед выполнением каждой
операции из последовательности
, составленную из операций типа
СОЗДАТЬ, ОБЪЕДИНИТЬ, НАЙТИ, назовем корректной, если перед выполнением каждой
операции из последовательности  соблюдены условия ее
применения. Например, перед выполнением очередной операции вида ОБЪЕДИНИТЬ
(
соблюдены условия ее
применения. Например, перед выполнением очередной операции вида ОБЪЕДИНИТЬ
(  ,
,  ) подмножества с именами
) подмножества с именами  и
и  должны
быть уже созданы. Перед выполнением операции СОЗДАТЬ(
должны
быть уже созданы. Перед выполнением операции СОЗДАТЬ(  ) элемент
) элемент  не
должен принадлежать ни одному из подмножеств коллекции. Операция НАЙТИ
(
не
должен принадлежать ни одному из подмножеств коллекции. Операция НАЙТИ
(  ,
,  ) применима при любом значении аргумента
) применима при любом значении аргумента  .
Следует только помнить, что если
.
Следует только помнить, что если  не принадлежит ни одному
из подмножеств коллекции, то получим
не принадлежит ни одному
из подмножеств коллекции, то получим  .
.
Мы рассмотрим несколько способов представления коллекции разделенных множеств в памяти компьютера и алгоритмической реализации перечисленных операций. А именно, будут описаны представления
- с помощью массива;
- с помощью древовидной структуры;
- с помощью древовидной структуры с использованием рангов вершин;
- с помощью древовидной структуры с использованием рангов вершин и сжатия путей.
Последний из перечисленных способов является наиболее эффективным по времени выполнения произвольных корректных последовательностей операций типа СОЗДАТЬ, ОБЪЕДИНИТЬ, НАЙТИ. Строго говоря, во всех перечисленных случаях будут использоваться массивы, но интерпретации их содержимого будут различными. Каждый раз при описании очередной реализации мы будем обсуждать оценки трудоемкости рассматриваемых операций.
