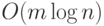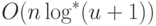|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Разделенные множества
Теорема 1.
Время выполнения последовательности операций,
состоящей из  операций СОЗДАТЬ,
операций СОЗДАТЬ,  операций
ОБЪЕДИНИТЬ и
операций
ОБЪЕДИНИТЬ и  операций НАЙТИ, при использовании
рангов и сжатия путей является величиной
операций НАЙТИ, при использовании
рангов и сжатия путей является величиной 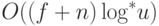 .
.
Доказательство
Пусть 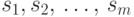 — все
операции вида СОЗДАТЬ, ОБЪЕДИНИТЬ, НАЙТИ, объявленные в формулировке
теоремы и выписанные в порядке их следования,
— все
операции вида СОЗДАТЬ, ОБЪЕДИНИТЬ, НАЙТИ, объявленные в формулировке
теоремы и выписанные в порядке их следования, 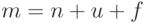 .
Очевидно, суммарная трудоемкость всех операций
СОЗДАТЬ есть
.
Очевидно, суммарная трудоемкость всех операций
СОЗДАТЬ есть  , суммарная трудоемкость всех операций
ОБЪЕДИНИТЬ есть
, суммарная трудоемкость всех операций
ОБЪЕДИНИТЬ есть 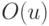 . Остается оценить суммарную трудоемкость
операций НАЙТИ.
. Остается оценить суммарную трудоемкость
операций НАЙТИ.
Через 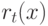 обозначим ранг узла
обозначим ранг узла  , который
получится после выполнения операции
, который
получится после выполнения операции  ,
а
,
а 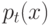 — родитель узла
— родитель узла  , получающийся
после выполнения этой операции. Определим множество
, получающийся
после выполнения этой операции. Определим множество

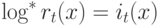 .
.Поскольку ранг узла может увеличиваться лишь при выполнении операции
ОБЪЕДИНИТЬ, причем не более чем на 1, после  таких операций ранг
никакого узла не может стать больше
таких операций ранг
никакого узла не может стать больше  , следовательно, максимальный
индекс
, следовательно, максимальный
индекс  , при котором
, при котором 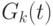 может быть непустым,
равен
может быть непустым,
равен 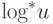 .
.
Оценим теперь суммарное время, требуемое для
выполнения  операций
НАЙТИ; очевидно, оно пропорционально числу ребер, ведущих от сыновей
к отцам и встречающихся при выполнении всех таких операций. Для оценки
времени, затрачиваемого на реализацию этих операций, применим
бухгалтерский прием. Отнесем расход времени на прохождение очередного
ребра
операций
НАЙТИ; очевидно, оно пропорционально числу ребер, ведущих от сыновей
к отцам и встречающихся при выполнении всех таких операций. Для оценки
времени, затрачиваемого на реализацию этих операций, применим
бухгалтерский прием. Отнесем расход времени на прохождение очередного
ребра  от узла
от узла  к его родителю
к его родителю  при
выполнении операции
при
выполнении операции 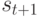 типа НАЙТИ на одну из трех разных
статей расходов: "корневую", "транзитную" и
"местную" в зависимости от
следующих условий.
типа НАЙТИ на одну из трех разных
статей расходов: "корневую", "транзитную" и
"местную" в зависимости от
следующих условий.
Если  и
и  в данный
момент не является корнем, то расходы относим на
статью
в данный
момент не является корнем, то расходы относим на
статью  транзитных
расходов. Если
транзитных
расходов. Если 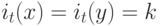 и
и  не является
корнем, то на статью
не является
корнем, то на статью 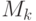 местных расходов
в
местных расходов
в  -м диапазоне, если же
-м диапазоне, если же  — корень, то на
статью
— корень, то на
статью  корневых расходов.
корневых расходов.
Сумму местных расходов во всех диапазонах обозначим через
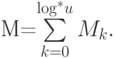
Имеем  , так как при каждом выполнении операции
НАЙТИ проходится одно корневое и, возможно, одно прикорневое ребро.
, так как при каждом выполнении операции
НАЙТИ проходится одно корневое и, возможно, одно прикорневое ребро.
Для транзитных переходов имеем 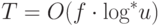 ,
так как при каждом выполнении операции НАЙТИ происходит не
более
,
так как при каждом выполнении операции НАЙТИ происходит не
более 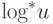 переходов из одного диапазона в другой.
переходов из одного диапазона в другой.
Для оценки величины  введем потенциал
введем потенциал  узла
узла  после выполнения
операции
после выполнения
операции  . Если к узлу
. Если к узлу  еще не применялась
операция СОЗДАТЬ, то
еще не применялась
операция СОЗДАТЬ, то 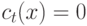 .
.
Потенциалом группы 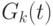 при текущем состоянии коллекции
назовем величину
при текущем состоянии коллекции
назовем величину

Очевидно, что в любой момент времени справедливо неравенство
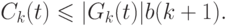 |
( 1) |
Покажем, что для любого узла  при любом
при любом 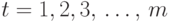 выполняется неравенство
выполняется неравенство 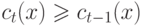 .
Действительно, если
.
Действительно, если  — операция СОЗДАТЬ (
— операция СОЗДАТЬ (  ),
то
),
то
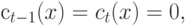
 , так же, как, очевидно, и всех остальных,
не изменяется. Пусть теперь
, так же, как, очевидно, и всех остальных,
не изменяется. Пусть теперь  — операция
ОБЪЕДИНИТЬ
— операция
ОБЪЕДИНИТЬ  .
.В случае  имеем
имеем
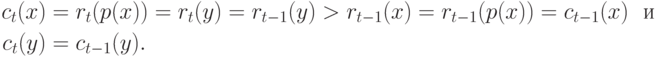
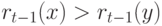 аналогичен.
аналогичен.В случае  имеем
имеем
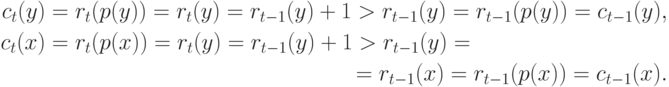
Пусть теперь  является операцией НАЙТИ, проходящей через
узел
является операцией НАЙТИ, проходящей через
узел  , и при этом
, и при этом 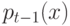 — не корень
(
— не корень
(  получает
нового родителя
получает
нового родителя 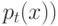 . Тогда имеем
. Тогда имеем
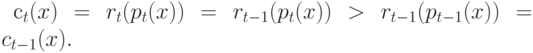
В этом случае совершен переход по внутреннему ребру (местный или транзитный).
Итак, для любого узла  величина
величина 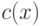 при выполнении
операции вида СОЗДАТЬ, ОБЪЕДИНИТЬ, НАЙТИ не может уменьшиться и,
следовательно,
при выполнении
операции вида СОЗДАТЬ, ОБЪЕДИНИТЬ, НАЙТИ не может уменьшиться и,
следовательно,

При этом, если  — операция НАЙТИ, то
у
— операция НАЙТИ, то
у  вершин при ее выполнении потенциал увеличится, по крайней
мере, на 1,
следовательно, число
вершин при ее выполнении потенциал увеличится, по крайней
мере, на 1,
следовательно, число  местных переходов в
группе
местных переходов в
группе 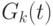 при ее выполнении удовлетворяет неравенству
при ее выполнении удовлетворяет неравенству

Суммируя это неравенство по всем  и учитывая неравенство (1),
получаем, что число
и учитывая неравенство (1),
получаем, что число 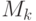 местных переходов при всех операциях
\mbox{НАЙТИ} удовлетворяет неравенству
местных переходов при всех операциях
\mbox{НАЙТИ} удовлетворяет неравенству

Заметим далее, что утверждение леммы 2, которая гарантирует,
что количество узлов ранга  не более
не более 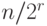 , остается
верным и при использовании сжатия путей, так как при выполнении операции НАЙТИ
ранги элементов не меняются. Следовательно, справедливы соотношения
, остается
верным и при использовании сжатия путей, так как при выполнении операции НАЙТИ
ранги элементов не меняются. Следовательно, справедливы соотношения

Отсюда

Итак, суммарная трудоемкость выполнения  операций НАЙТИ
равна
операций НАЙТИ
равна
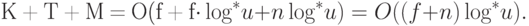
Замечание. Используя функцию Аккермана, задаваемую равенствами
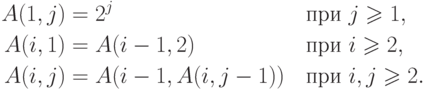
и обратную к ней функцию

Р.Е.Тарьян доказал, что время выполнения последовательности,
состоящей из  операций ОБЪЕДИНИТЬ с перемешанными
с ними
операций ОБЪЕДИНИТЬ с перемешанными
с ними  операциями НАЙТИ, где
операциями НАЙТИ, где  ,
, 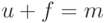 ,
является величиной
,
является величиной  . Также он показал,
что эта оценка не может быть улучшена, то есть алгоритм может потребовать
для своего выполнения
. Также он показал,
что эта оценка не может быть улучшена, то есть алгоритм может потребовать
для своего выполнения  времени.
времени.
Сводные данные о сложности операций с разделенными множествами
Реализация с помощью массива
Реализация с помощью древовидной cтруктуры
Реализация с использованием рангов вершин
Реализация с использованием рангов и сжатия путей



 операций
операций