|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Биномиальные и фибоначчиевы кучи
Биномиальные кучи
Для каждого 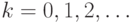 биномиальное
дерево
биномиальное
дерево 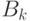 определяется следующим образом:
определяется следующим образом: 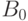 — дерево, состоящее
из одного узла высоты
— дерево, состоящее
из одного узла высоты  ; далее при
; далее при 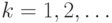 дерево
дерево 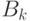 высоты
высоты  формируется из двух деревьев
формируется из двух деревьев 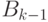 , при
этом корень одного из них становится потомком корня другого. На рис. 7.1
изображены биномиальные деревья
, при
этом корень одного из них становится потомком корня другого. На рис. 7.1
изображены биномиальные деревья 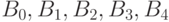 .
.
Биномиальный лес — это набор биномиальных деревьев, в котором любые два дерева имеют разные высоты.
Свойства биномиальных деревьев
- Дерево
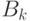 состоит из корня с присоединенными к нему
корнями поддеревьев
состоит из корня с присоединенными к нему
корнями поддеревьев  в указанном порядке.
в указанном порядке. - Дерево
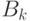 имеет высоту
имеет высоту  .
. - Дерево
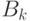 имеет ровно
имеет ровно 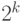 узлов.
узлов. - В дереве
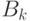 на глубине
на глубине  имеется ровно
имеется ровно 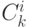 узлов.
узлов. - В дереве
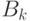 корень имеет степень
корень имеет степень  , остальные
узлы имеют меньшую степень.
, остальные
узлы имеют меньшую степень. - Для каждого натурального числа n существует
биномиальный лес, в котором количество узлов равно
 .
. - Максимальная степень вершины в биномиальном лесе с
 узлами равна
узлами равна  .
. -
Биномиальный лес содержит не более
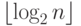 биномиальных поддеревьев.
биномиальных поддеревьев.
Чтобы убедиться в существовании биномиального леса из  узлов,
представим
узлов,
представим  в двоичной системе счисления (разложим по степеням
двойки)
в двоичной системе счисления (разложим по степеням
двойки)  ,
где
,
где 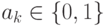 . Для каждого
. Для каждого 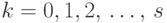 ,
такого, что
,
такого, что 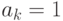 , в искомый лес включаем
дерево
, в искомый лес включаем
дерево 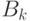 .
.
Биномиальная куча — это набор биномиальных деревьев, узлам которых приписаны элементы взвешенного множества в соответствии с кучеобразным порядком, при котором вес элемента, приписанного узлу, не превосходит весов элементов, приписанных его потомкам.
Поскольку количество детей у узлов варьируется в широких пределах, ссылка на детей осуществляется через левого ребенка, а остальные дети образуют односвязный список. Каждый узел в биномиальной куче представляется набором полей
![\eq*{
[{\rm key}, {\rm parent}, {\rm child}, {\rm sibling}, {\rm degree}],
}](/sites/default/files/tex_cache/082040e2a70e0bdd16c40b944dc1d1b6.png)
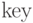 — ключ (вес) элемента, приписанного узлу,
— ключ (вес) элемента, приписанного узлу,  — родитель узла,
— родитель узла,  — левый ребенок
узла,
— левый ребенок
узла,  — правый брат узла,
— правый брат узла,  — степень узла.
— степень узла.Доступ к куче осуществляется ссылкой на самое левое поддерево. Корни
деревьев, из которых составлена куча, оказываются организованными
с помощью поля  в так называемый корневой
односвязный список.
в так называемый корневой
односвязный список.
Поиск элемента с минимальным ключом. Поскольку искомый элемент
находится в корне одного из деревьев кучи, элемент с минимальным ключом
находится путем просмотра корневого списка за время  .
.
Слияние двух очередей.
Две очереди  и
и  объединяются в одну
очередь
объединяются в одну
очередь  следующим образом. Последовательно
выбираются деревья из исходных очередей в порядке возрастания их высот
и вставляются в результирующую очередь
следующим образом. Последовательно
выбираются деревья из исходных очередей в порядке возрастания их высот
и вставляются в результирующую очередь  , вначале пустую.
, вначале пустую.
Если дерево  очередной высоты
очередной высоты  присутствует
лишь в одной из исходных очередей, то перемещаем его в результирующую очередь.
Если оно присутствует в одной из исходных очередей и уже есть
в результирующей очереди, то объединяем эти деревья
в одно
присутствует
лишь в одной из исходных очередей, то перемещаем его в результирующую очередь.
Если оно присутствует в одной из исходных очередей и уже есть
в результирующей очереди, то объединяем эти деревья
в одно  ,
которое вставляем в
,
которое вставляем в  . Если
. Если  присутствует во всех
трех очередях, то сливаем два из них в
присутствует во всех
трех очередях, то сливаем два из них в  и вставляем в
и вставляем в  , а третье дерево
, а третье дерево  просто
перемещаем в
просто
перемещаем в  . Трудоемкость —
. Трудоемкость —  .
.
Вставка нового элемента. Создается одноэлементная очередь из
вставляемого элемента, которая объединяется с исходной очередью.
Трудоемкость —  .
.
Удаление минимального
элемента. Сначала в исходной куче  производится поиск дерева
производится поиск дерева 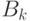 , имеющего корень с минимальным
ключом. Найденное дерево удаляется из
, имеющего корень с минимальным
ключом. Найденное дерево удаляется из  , его прикорневые
поддеревья
, его прикорневые
поддеревья  включаются в новую очередь
включаются в новую очередь  ,
которая объединяется с исходной очередью
,
которая объединяется с исходной очередью  .
Трудоемкость —
.
Трудоемкость —  .
.
Уменьшение ключа. Осуществляется
с помощью всплытия. Трудоемкость —  .
.
Удаление элемента.
Уменьшается ключ удаляемого элемента
до  , применяется всплытие, всплывший элемент удаляется как
минимальный. Трудоемкость —
, применяется всплытие, всплывший элемент удаляется как
минимальный. Трудоемкость —  .
.

