Поисковые деревья

Двоичные деревья поиска

Общие сведения

Деревья поиска предназначены для представления словарей как абстрактного типа данных. Как и приоритетные очереди, они представляют взвешенные множества, но с другим набором операций, а именно:

• Search — поиск элемента с заданным ключом.
• Minimum — поиск элемента с минимальным ключом.
• Maximum — поиск элемента с максимальным ключом.
• Predecessor — поиск элемента с предыдущим ключом.
• Successor — поиск элемента со следующим ключом.
• Insert — вставка элемента со своим ключом.
• Delete — удаление указанного элемента.

Считается, что каждый элемент словаря имеет ключ (вес), принимающий значение из какого-либо линейно упорядоченного множества. Таким множеством может быть, например, числовое множество или множество слов в некотором алфавите. В последнем случае в качестве линейного порядка можно рассматривать лексикографический порядок. Таким образом, дерево поиска может быть использовано и как словарь, и как приоритетная очередь.

Время выполнения основных операций пропорционально высоте дерева. Если каждый внутренний узел двоичного дерева имеет ровно двух потомков, то его высота и время выполнения основных операций пропорциональны логарифму числа узлов. Напротив, если дерево представляет собой линейную цепочку из узлов, это время вырастает до . Известно, что высота случайного двоичного дерева поиска есть , так что в этом случае время выполнения основных операций есть .

Конечно, возникающие на практике двоичные деревья поиска могут быть далеки от случайных. Однако, приняв специальные меры по балансировке деревьев, мы можем гарантировать, что высота деревьев с узлами будет . Ниже рассмотрим один из подходов такого рода (красно-черные деревья и, как частный случай, АВЛ-деревья). Будут рассмотрены также Б-деревья, которые особенно удобны для данных, хранящихся во вторичной памяти с произвольным доступом (на диске).

Представление двоичных деревьев поиска

Двоичным деревом поиска называется корневое двоичное дерево, каждому узлу которого поставлен в соответствие взвешенный элемент. При этом для каждого узла выполняется следующее условие:

Веса всех узлов левого поддерева в дереве с корнем меньше, а веса узлов его правого поддерева больше веса узла или равны ему.

Представляется такое дерево узлами следующего вида:

Доступ к дереву осуществляется с помощью ссылки 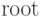.