|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Поисковые деревья
Операции с двоичным поисковым деревом
Процедура 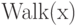 обходит все узлы поддерева с корнем в узле
обходит все узлы поддерева с корнем в узле  и печатает их ключи в
неубывающем порядке:
и печатает их ключи в
неубывающем порядке:
![\formula{
\t pocedure\ \t{Walk}(x);\\
\t begin\\
\mbox{}\q \t if\ (x \ne {\rm nil})\
\t then\
\{{\rm Walk}({\rm left}[x]);\ {\rm write}({\rm key}[x]);\ {\rm Walk}
({\rm right}[x])\}\\
\t end;
}](/sites/default/files/tex_cache/790026e2b83857a7e6ab835a333e7f59.png)
Свойство упорядоченности гарантирует правильность алгоритма. Время работы
на дереве с  вершинами есть
вершинами есть  , каждая вершина
обрабатывается один раз. Оператор
, каждая вершина
обрабатывается один раз. Оператор  напечатает
ключи всех элементов в неубывающем порядке.
напечатает
ключи всех элементов в неубывающем порядке.
Заметим, что порядок, при котором корень предшествует узлам обоих поддеревьев, называется preorder ; порядок, в котором корень следует за ними, называется postorder.
Покажем, что двоичные поисковые деревья позволяют выполнять
операции  ,
,  ,
,  ,
,  и
и 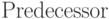 за
время (
за
время ( 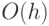 , где
, где  — высота дерева.
— высота дерева.
Поиск.
Процедура поиска получает на вход
искомый ключ  и указатель
и указатель  на корень дерева и
возвращает указатель на вершину с ключом
на корень дерева и
возвращает указатель на вершину с ключом  (если такая есть) или
(если такая есть) или  (если такой вершины нет).
(если такой вершины нет).
![\formula{
\t procedure\ {\rm Search}\ (x,
k);\\
\t begin\\
\mbox{}\q\t if\ (x = {\rm nil})\
\t{or}\ (k = {\rm key}[x])\
\t then\ {\rm exit};\\
\mbox{}\q\t if\ (k < {\rm key}[x])\
\t then\
{\rm Search}\ ({\rm left}[x], k)\ \t else\ {\rm Search}({\rm right}[x],
k)\\
\t end;
}](/sites/default/files/tex_cache/d34ac9094eabc3697b5fdde05f67114f.png)
В процессе поиска мы двигаемся от корня, сравнивая ключ  с ключом,
хранящимся в текущей вершине
с ключом,
хранящимся в текущей вершине  . Если они равны, поиск завершается.
Если
. Если они равны, поиск завершается.
Если ![k < {\rm key}[x]](/sites/default/files/tex_cache/188867470a145daa66f9c6c6a6752892.png) , то поиск продолжается в левом
поддереве
, то поиск продолжается в левом
поддереве  , если же
, если же ![k > {\rm key}[x]](/sites/default/files/tex_cache/15057bccc0b138a54ec740e25d7c7aad.png) , то в правом.
Длина пути поиска не превосходит высоты дерева, поэтому время
поиска есть
, то в правом.
Длина пути поиска не превосходит высоты дерева, поэтому время
поиска есть 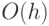 (где
(где  — высота дерева).
— высота дерева).
Итеративная версия процедуры Поиск
![\formula{
\t procedure\ {\rm
IterativeSearch}\ (x,k);\\
\t begin\\
\mbox{}\q\t while\ (x \ne {\rm
nil})\ \t{and}\ (k \ne {\rm key}[x])\ \t do\\
\mbox{}\qq\t if\ k < {\rm key}[x]\
\t then\ x:= {\rm left}[x]\
\t else\ x:= {\rm right}[x];\\
\t end;
}](/sites/default/files/tex_cache/b01c04b8d78696e57fb42d57976aee4f.png)
Минимум и Максимум.
Элемент с минимальным ключом в дереве поиска
можно найти, пройдя от корня по указателям  , пока не
упремся в
, пока не
упремся в  . Процедура
. Процедура  возвращает
указатель на найденный элемент поддерева с корнем
возвращает
указатель на найденный элемент поддерева с корнем  .
.
![\formula{
\t procedure\ {\rm Minimum}(x);\\
\t begin\ \t while\ {\rm left}[x] \ne {\rm nil}\ \t do\
x:= {\rm left}[x]\ \t end;
}](/sites/default/files/tex_cache/c50926b93b88e45ec3a952999c58f21b.png)
![\formula{
\t procedure\ {\rm Maximum}(x);\\
\t begin\ \t while\ {\rm right}[x] \ne {\rm nil}\ \t do\
x:= {\rm right}[x]\ \t end;
}](/sites/default/files/tex_cache/2b05bb76d3b4a74a4dee3e105805ed20.png)
Оба алгоритма требуют времени 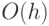 , где
, где  —
высота дерева.
—
высота дерева.
Следующий и
предыдущий элементы. Если  — указатель на
некоторый узел дерева, то процедура
— указатель на
некоторый узел дерева, то процедура  возвращает
указатель на узел со следующим за
возвращает
указатель на узел со следующим за  элементом или
элементом или  , если указанный элемент — последний в дереве:
, если указанный элемент — последний в дереве:
![\formula{
\t procedure\ {\rm
Successor}(x);\\
\t begin\\
\mbox{}\q\t if\ ({\rm right}[x] \ne
{\rm nil})\ \t then\ {\rm return}\
{\rm Minimum}\ ({\rm right}[x]);\\
\mbox{}\q y:= p[x];\\
\mbox{}\q \t while\ (y \ne {\rm
nil})\ \t{and}\ (x={\rm right}[y])\
\t do\ \{x:= y;\ y:= {\rm
parent}[y]\};\\
\mbox{}\q{\rm return}\ y\\
\t end;
}](/sites/default/files/tex_cache/fc46ea32ed125e2b1b53e6f9c07840f8.png)
Приведенная процедура отдельно рассматривает два случая. Если правое
поддерево вершины  не пусто, то следующий
за
не пусто, то следующий
за  элемент —
минимальный элемент в этом поддереве и он равен
элемент —
минимальный элемент в этом поддереве и он равен ![{\rm Minimum}({\rm
right}[x])](/sites/default/files/tex_cache/91ac7075e01e99e022ecc28cc049bbda.png) . Если правое поддерево
вершины
. Если правое поддерево
вершины  пусто, то идем от
пусто, то идем от  вверх, пока не
найдем вершину, являющуюся левым сыном своего
родителя. Этот родитель (если он есть) и будет искомым элементом. Время
работы процедуры
вверх, пока не
найдем вершину, являющуюся левым сыном своего
родителя. Этот родитель (если он есть) и будет искомым элементом. Время
работы процедуры  на дереве
высоты
на дереве
высоты  есть
есть 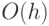 ,
так как мы двигаемся либо только вверх, либо только вниз.
Процедура
,
так как мы двигаемся либо только вверх, либо только вниз.
Процедура 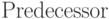 симметрична.
симметрична.
Добавление элемента.
Процедура  добавляет заданный элемент в подходящее место дерева
добавляет заданный элемент в подходящее место дерева  .
Параметром процедуры является указатель
.
Параметром процедуры является указатель  на новую вершину,
в которую помещены значения
на новую вершину,
в которую помещены значения ![{\rm key}[z]](/sites/default/files/tex_cache/78fefc4bb9588835852e7aad0f76e08f.png) ,
, ![{\rm left}[z] = {\rm
nil}](/sites/default/files/tex_cache/ad3815e18efde40e1a0dfa6cde839ea9.png) и
и ![{\rm right}[z] = {\rm nil}](/sites/default/files/tex_cache/b8fd80b0ca576a015652ad0e5b13d562.png) . В ходе работы процедура
изменяет дерево
. В ходе работы процедура
изменяет дерево  и (возможно) некоторые поля
вершины
и (возможно) некоторые поля
вершины  , после чего новая вершина
с данным значением ключа оказывается вставленной в подходящее место дерева:
, после чего новая вершина
с данным значением ключа оказывается вставленной в подходящее место дерева:
![\formula{
\t procedure\ {\rm
Insert}(T,z);\\
begin y := {\rm nil};\ x := {\rm
root};\\
\mbox{}\q\t while\ (x \ne {\rm
nil})\ \t do\\
\mbox{}\q\q \{y := x;\ \t if\ {\rm
key}[z] < {\rm key}[x]\
\t then\ x := {\rm left}[x]\
\t else\ x := {\rm right}[x]\};\\
\mbox{}\q p[z] := y;\\
\mbox{}\q \t if\ y = {\rm nil}\
\t then\
{\rm root} := z \t else\ \t if\ {\rm key}[z] < {\rm key}[y]\
\t then\ {\rm left}[y] := z\
\t else\\
\mbox{}\q\q {\rm right}[y]:= z\\
\t end;
}](/sites/default/files/tex_cache/5cd4be4a34c0b673838908e3db5c1743.png)
Подобно процедурам  и
и  ,
процедура
,
процедура  двигается вниз по дереву, начав
с его корня. При этом в вершине
двигается вниз по дереву, начав
с его корня. При этом в вершине  сохраняется указатель
на родителя вершины
сохраняется указатель
на родителя вершины  . Сравнивая
. Сравнивая ![{\rm
key}[z]](/sites/default/files/tex_cache/fb9359b1f9f487a6310222de043fde7f.png) с
с ![{\rm key}[x]](/sites/default/files/tex_cache/a20e6cbf254bfa2fd9db64c2d9e9e544.png) , процедура решает куда идти —
налево или направо. Процесс завершается, когда
, процедура решает куда идти —
налево или направо. Процесс завершается, когда  становится
равным
становится
равным  . Этот
. Этот  стоит как раз там,
куда надо поместить
стоит как раз там,
куда надо поместить  , что и делается.
Очевидно, добавление требует времени
, что и делается.
Очевидно, добавление требует времени 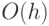 для дерева
высоты
для дерева
высоты  .
.
Удаление элемента
Параметром процедуры удаления является указатель  на удаляемую
вершину. При удалении возможны три случая. Если у
на удаляемую
вершину. При удалении возможны три случая. Если у  нет детей, для
удаления
нет детей, для
удаления  достаточно поместить
достаточно поместить 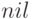 в соответствующее поле его
родителя вместо
в соответствующее поле его
родителя вместо  . Если у
. Если у  есть один ребенок, можно
вырезать
есть один ребенок, можно
вырезать  ,
соединив его родителя напрямую с его ребенком. Если же детей
двое, находим следующий за
,
соединив его родителя напрямую с его ребенком. Если же детей
двое, находим следующий за  элемент
элемент  ; у него нет
левого ребенка. Теперь можно скопировать ключ и дополнительные данные
из вершины
; у него нет
левого ребенка. Теперь можно скопировать ключ и дополнительные данные
из вершины  в вершину
в вершину  , а саму
вершину
, а саму
вершину  удалить описанным выше способом.
удалить описанным выше способом.
Упражнения
- Напишите рекурсивный вариант процедуры
 .
. - Напишите процедуру
 , удаляющую
элемент
, удаляющую
элемент  из дерева
из дерева  .
. - Набор из
 чисел можно отсортировать, сначала добавив их один
за другим в двоичное дерево поиска с помощью процедуры
чисел можно отсортировать, сначала добавив их один
за другим в двоичное дерево поиска с помощью процедуры  ,
а потом обойти дерево с помощью процедуры
,
а потом обойти дерево с помощью процедуры  . Оцените время работы
такого алгоритма.
. Оцените время работы
такого алгоритма. - Покажите, что если вершина двоичного дерева поиска имеет двоих детей, то следующая за ней вершина не имеет левого ребенка, а предшествующая — правого.

 симметричен:
симметричен: