|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Объединяемые приоритетные очереди
Левосторонние кучи
Левосторонняя куча — это представление приоритетной очереди с помощью так называемого левостороннего бинарного дерева. При реализации приоритетных очередей левосторонними кучами предусматривается возможность их объединения.
Бинарным деревом называется корневое дерево, у которого каждый узел имеет не более двух непосредственных потомков. Один из потомков называется левым, другой, если он есть, — правым. Узел называется неполным, если он имеет менее двух непосредственных потомков. В частности, листья дерева являются неполными узлами.
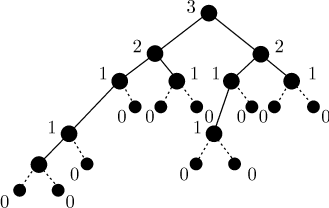
Рангом узла будем называть увеличенное на 1 расстояние (число ребер) от него до ближайшего неполного потомка.
Ранг узла также можно определить следующим образом. Расширить данное дерево до полного бинарного дерева, добавляя к каждому узлу, имеющему менее двух потомков, в том числе и к листьям исходного дерева, недостающее количество потомков. Затем приписать каждому из листьев полученного расширенного дерева ранг 0, а ранг каждого из остальных узлов определить как минимум из рангов его непосредственных потомков плюс 1. Очевидно, что ранги вершин исходного дерева совпадут с рангами соответствующих вершин расширенного дерева.
Левостороннее дерево — это бинарное дерево, для каждого узла которого ранг его левого непосредственного потомка в расширенном дереве не меньше ранга его правого потомка.
Ветвью бинарного дерева мы называем последовательность его узлов, начинающуюся с корня и заканчивающуюся листом, такую, что каждый следующий узел является непосредственным потомком предыдущего.
Правой ветвью дерева мы называем ветвь, заканчивающуюся в узле, не имеющем правого потомка, такую, что каждый следующий узел является непосредственным правым потомком предыдущего.
Пример левостороннего дерева (и его расширения) приведен на рис. 5.1. Ребра исходного дерева выделены жирными линиями, а ребра, добавленные при расширении, — пунктиром. Числа рядом с узлами — их ранги.
Свойства левостороннего дерева
- Правая ветвь из любого узла дерева имеет минимальную длину среди всех ветвей, исходящих из этого узла.
- Длина правой ветви левостороннего дерева, имеющего
 узлов,
ограничена величиной
узлов,
ограничена величиной  ,
,  .
.
Первое свойство непосредственно следует из определения левостороннего
дерева. Для доказательства второго свойства рассмотрим левостороннее
дерево  , у которого длина правой ветви равна
, у которого длина правой ветви равна  .
Индукцией по числу
.
Индукцией по числу  докажем, что число
докажем, что число  узлов в таком дереве
удовлетворяет неравенству
узлов в таком дереве
удовлетворяет неравенству 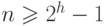 . Действительно,
при
. Действительно,
при 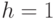 утверждение очевидно. При
утверждение очевидно. При 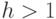 левое и правое
поддеревья дерева
левое и правое
поддеревья дерева  будут левосторонними, а ранги их корней больше
или равны
будут левосторонними, а ранги их корней больше
или равны 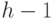 . Следовательно, по предположению индукции число
узлов в каждом из них больше или равно
. Следовательно, по предположению индукции число
узлов в каждом из них больше или равно 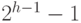 ,
а в дереве
,
а в дереве  — больше или равно
— больше или равно
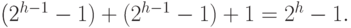
Для реализации приоритетной очереди с помощью левосторонней кучи будем использовать узлы вида

- element — элемент приоритетной очереди или ссылка на него (используется прикладной программой);
- key — его ключ (вес);
- rank — ранг узла, которому приписан рассматриваемый элемент;
- left, right — указатели на левое и правое поддеревья;
- parent — указатель на родителя.
Куча представляется указателем на ее корень. Если  —
указатель на
корень кучи, то через
—
указатель на
корень кучи, то через  будем обозначать и саму кучу. Заметим, что
указатель на родителя используется лишь в операциях УДАЛИТЬ и УМЕНЬШИТЬ_КЛЮЧ (см.
ниже).
будем обозначать и саму кучу. Заметим, что
указатель на родителя используется лишь в операциях УДАЛИТЬ и УМЕНЬШИТЬ_КЛЮЧ (см.
ниже).