|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Объединяемые приоритетные очереди
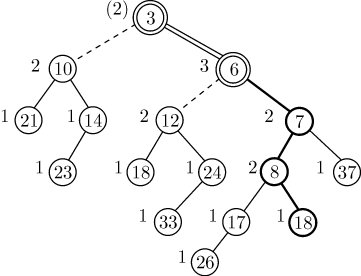
Далее рассматриваем узел с ключом 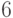 . Оба его сына имеют
одинаковый ранг
. Оба его сына имеют
одинаковый ранг  ,
следовательно, менять их местами не требуется. Вычислим лишь новое
значение ранга: оно равно минимальному из рангов его детей (рангу правого
сына) плюс~
,
следовательно, менять их местами не требуется. Вычислим лишь новое
значение ранга: оно равно минимальному из рангов его детей (рангу правого
сына) плюс~  , то есть
, то есть  . Получаем дерево,
изображенное на рис.5.6.
. Получаем дерево,
изображенное на рис.5.6.
Наконец, рассматриваем узел с ключом  , который является
последним в правой ветви, полученной слиянием правых ветвей исходных куч. Его потомков
(узлы с ключами
, который является
последним в правой ветви, полученной слиянием правых ветвей исходных куч. Его потомков
(узлы с ключами  и
и 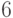 ) необходимо поменять местами
для восстановления
свойства левизны и обновить ранг, который будет теперь равен
) необходимо поменять местами
для восстановления
свойства левизны и обновить ранг, который будет теперь равен  .
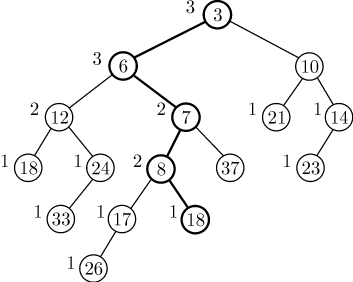
После выполнения этих операций получим левостороннюю кучу, изображенную
на рис.5.7.
На этом выполнение операции СЛИЯНИЕ заканчивается.
.
После выполнения этих операций получим левостороннюю кучу, изображенную
на рис.5.7.
На этом выполнение операции СЛИЯНИЕ заканчивается.
Очевидно, время выполнения операции СЛИЯНИЕ пропорционально сумме длин
правых путей сливаемых куч. По свойству левосторонней кучи оно не
превосходит величины 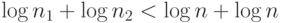 , где
, где  ,
, 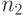 — количества узлов
в исходных кучах,
а
— количества узлов
в исходных кучах,
а 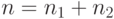 — количество узлов в результирующей куче.
Следовательно, вычислительная сложность операции СЛИЯНИЕ равна
— количество узлов в результирующей куче.
Следовательно, вычислительная сложность операции СЛИЯНИЕ равна  .
.
Реализация операции СЛИЯНИЕ
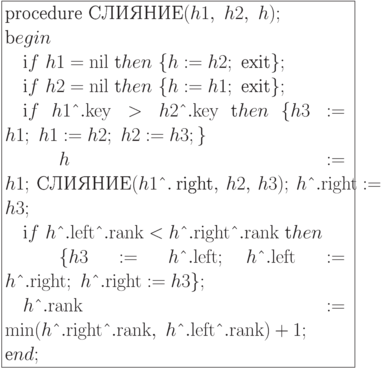
Операция ВСТАВКА. Эта операция позволяет осуществить
вставку в кучу  нового элемента
нового элемента  с ключом
с ключом  .
Она производится посредством образования левосторонней кучи,
содержащей единственный элемент
.
Она производится посредством образования левосторонней кучи,
содержащей единственный элемент  с ключом
с ключом  ,
и слияния ее с кучей
,
и слияния ее с кучей  . Вычислительную сложность
данной операции можно оценить так же, как вычислительную
сложность операции СЛИЯНИЕ, то есть
величиной
. Вычислительную сложность
данной операции можно оценить так же, как вычислительную
сложность операции СЛИЯНИЕ, то есть
величиной  .
.
Реализация операции ВСТАВКА
![\formula{
\t{ procedure
ВСТАВКА}(x,\,k,\,h);\\
\t begin\\
\mbox{}\q {\rm CREATE}\ {\rm node}\ h1:
[\t{element}, \t{key}, \t{rank}, \t{left}, \t{right}, \t{parent}]
= [x, k, l,\\
\mbox{}\q {\rm nil}, {\rm nil}, {\rm nil}];\\
\mbox{}\q \t{СЛИЯНИЕ}(h,\,h1,\,h2);\ h := h2\\
\t end;
}](/sites/default/files/tex_cache/6c109842bf626fcc33201333c2adba08.png)
Операция
УДАЛЕНИЕ_МИНИМУМА. Эта операция позволяет из кучи  удалить элемент с минимальным ключом. Она
производится посредством удаления корня кучи
удалить элемент с минимальным ключом. Она
производится посредством удаления корня кучи  (трудоемкость
(трудоемкость  ),
а затем слияния его левой и правой подкуч (трудоемкость
),
а затем слияния его левой и правой подкуч (трудоемкость  ).
Таким образом, вычислительная сложность данной операции является
величиной
).
Таким образом, вычислительная сложность данной операции является
величиной  .
.
Реализация операции УДАЛЕНИЕ_МИНИНИМУМА

Операция МИНИМУМ. Эта операция позволяет
взять из кучи  элемент с минимальным ключом, не удаляя
его из кучи. Поскольку элемент с минимальным ключом находится
в корне кучи, требуется лишь скопировать его в нужное место.
Вычислительная сложность данной операции
элемент с минимальным ключом, не удаляя
его из кучи. Поскольку элемент с минимальным ключом находится
в корне кучи, требуется лишь скопировать его в нужное место.
Вычислительная сложность данной операции  .
.
Реализация операции МИНИМУМ
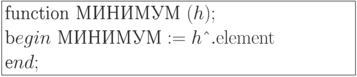
Операция УДАЛЕНИЕ.
Эта операция позволяет удалить из кучи  элемент
элемент  , расположенный в узле, заданном
позицией
, расположенный в узле, заданном
позицией  . Удаление может быть проведено
в несколько этапов.
. Удаление может быть проведено
в несколько этапов.
- Если узел
 является корнем
кучи
является корнем
кучи  , то применяется операция
УДАЛЕНИЕ_МИНИМУМА из кучи
, то применяется операция
УДАЛЕНИЕ_МИНИМУМА из кучи  . Иначе выполняются следующие
действия.
. Иначе выполняются следующие
действия. - От исходной кучи
 отрывается подкуча
отрывается подкуча 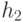 с корнем в удаляемом узле
с корнем в удаляемом узле  . Оставшаяся куча, для которой сохраняем
обозначение
. Оставшаяся куча, для которой сохраняем
обозначение  , не обязательно является левосторонней.
, не обязательно является левосторонней. - Затем узел
 удаляется из кучи
удаляется из кучи 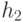 , а его левая
и правая подкучи сливаются в одну кучу
, а его левая
и правая подкучи сливаются в одну кучу 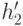 (время выполнения —
(время выполнения —  , как доказано выше).
, как доказано выше). - Куча
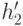 делается таким же сыном узла
делается таким же сыном узла  (
(  —
родитель узла
—
родитель узла  ), каким являлся для нее узел
), каким являлся для нее узел  (левым или правым).
(левым или правым). - Наконец, в куче
 восстанавливается свойство левизны.
Фактически свойству левизны могут не удовлетворять только узлы, находящиеся на пути
от
восстанавливается свойство левизны.
Фактически свойству левизны могут не удовлетворять только узлы, находящиеся на пути
от  к корню кучи
к корню кучи  . Длина этого пути в худшем
случае может линейно зависеть от
. Длина этого пути в худшем
случае может линейно зависеть от  . Но на самом деле нам нужно проверить только
первые не более чем
. Но на самом деле нам нужно проверить только
первые не более чем 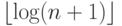 узлов на этом пути (потому что максимальный по длине правый
путь имеет максимум
узлов на этом пути (потому что максимальный по длине правый
путь имеет максимум 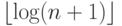 узлов).
узлов).