Объединяемые приоритетные очереди

Рассмотрим пример выполнения данной операции. Пусть из кучи , изображенной на рис. 5.8, необходимо удалить элемент с ключом .

Рис. 5.8.

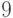Сначала отрывается подкуча 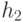с корнем . От остаются куча (нелевосторонняя, так как свойству левизны не удовлетворяет узел ) и левосторонняя куча 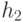(рис. 5.9).

Рис. 5.9.

Затем удаляется узел , а его левая и правая подкуч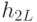и и 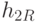сливаются в одну кучу 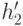при помощи описанной выше операции СЛИЯНИЕ; см. рис. 5.10.

Рис. 5.10.

Поскольку узел не являлся корнем кучи , операция еще не завершена. Куча 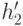становится левым поддеревом узла , так как узел был его левым сыном (рис. 5.11).

Рис. 5.11.

Следуем от узла к корню дерева, для каждого узла этого пути восстанавливаем свойство левизны и ранг. Сначала проверяем узел : его детей надо поменять местами, так как ранг узла с ключом (он равен ) меньше ранга узла с ключом 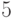(он равен ). После этого обновляется ранг узла : он равен рангу правого сына плюс , то есть . Получилось дерево, изображенное на рис. 5.12.

Рис. 5.12.

Следующий узел на пути к корню — это родитель узла с ключом, равным 2. Ранги его сыновей равны, значит менять их местами не нужно. Однако его собственный ранг, возможно, требует обновления, новое значение равно рангу его правого сына плюс 1, т.е. старому: . В результате получается дерево, изображенное на рис. 5.13.

Рис. 5.13.

Поскольку узел с ключом является корнем дерева, операция УДАЛЕНИЕ завершена.

Реализация операции УДАЛЕНИЕ