|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Объединяемые приоритетные очереди
Операция УМЕНЬШИТЬ_КЛЮЧ.
Ключ узла  , находящегося в дереве
в позиции
, находящегося в дереве
в позиции  , уменьшается на положительное число
, уменьшается на положительное число  .
Это действие может нарушить кучеобразный порядок
лишь таким образом, что уменьшенный
ключ узла
.
Это действие может нарушить кучеобразный порядок
лишь таким образом, что уменьшенный
ключ узла  будет меньше ключа его родителя. Уменьшение ключа
может быть проведено в несколько этапов.
будет меньше ключа его родителя. Уменьшение ключа
может быть проведено в несколько этапов.
От исходной кучи  отрывается подкуча
отрывается подкуча 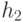 с
корнем в узле
с
корнем в узле  .
Оставшаяся куча
.
Оставшаяся куча  не обязательно будет левосторонней. Затем ключ
узла
не обязательно будет левосторонней. Затем ключ
узла  уменьшается на заданное число
уменьшается на заданное число  .
Куча
.
Куча 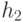 при этом все еще остается левосторонней.
при этом все еще остается левосторонней.
В куче  восстанавливается свойство левизны, как —
показано далее.
Фактически свойству левизны могут не удовлетворять только узлы,
находящиеся на пути от
восстанавливается свойство левизны, как —
показано далее.
Фактически свойству левизны могут не удовлетворять только узлы,
находящиеся на пути от  (
(  — родитель узла
— родитель узла  ) до корня
) до корня  .
Длина этого пути в худшем случае линейно зависит от
.
Длина этого пути в худшем случае линейно зависит от  .
Но на самом деле нам нужно проверить только первые
не более чем
.
Но на самом деле нам нужно проверить только первые
не более чем 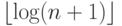 узлов на этом пути.
Наконец, куча
узлов на этом пути.
Наконец, куча  сливается с
сливается с 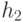 за
время
за
время  . Таким образом, время выполнения данной
операции —
. Таким образом, время выполнения данной
операции —  .
.
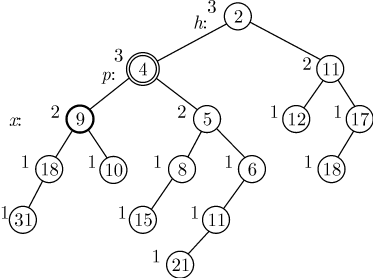
Рассмотрим пример. Пусть в куче, изображенной на рис. 5.14,
необходимо уменьшить ключ узла  от
от 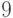 до
до  .
.
Делается это следующим образом. От исходной кучи  отрывается
подкуча
отрывается
подкуча 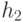 с корнем в удаляемом узле
с корнем в удаляемом узле  . Теперь
куча
. Теперь
куча  не
является левосторонней, так как в узле
не
является левосторонней, так как в узле  нарушено свойство
левизны (рис. 5.15).
нарушено свойство
левизны (рис. 5.15).
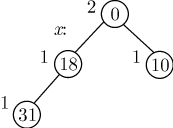
Ключ узла  уменьшается до 0, куча
уменьшается до 0, куча 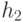 при этом
все еще остается левосторонней (рис. 5.16).
при этом
все еще остается левосторонней (рис. 5.16).
Следуем от узла  до корня дерева
до корня дерева  , для каждого
узла этого пути восстанавливаем свойство левизны и ранг.
Сначала проверяем узел
, для каждого
узла этого пути восстанавливаем свойство левизны и ранг.
Сначала проверяем узел  : его детей надо поменять местами
(а фактически — только
одного-единственного правого сына сделать левым). После этого вычисляется
новый ранг узла
: его детей надо поменять местами
(а фактически — только
одного-единственного правого сына сделать левым). После этого вычисляется
новый ранг узла  : он равен рангу правого сына плюс 1, то есть 1
(так как правого сына нет). Получилось дерево, изображенное
на рис. 5.17.
: он равен рангу правого сына плюс 1, то есть 1
(так как правого сына нет). Получилось дерево, изображенное
на рис. 5.17.
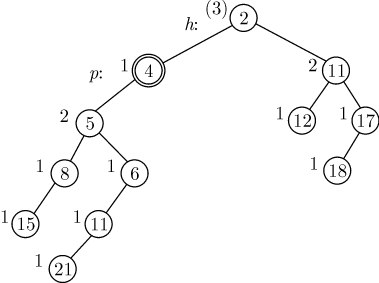
Следующий узел — это родитель узла  с ключом
с ключом  . Его потомков тоже
необходимо поменять местами (так как ранг левого сына меньше ранга
правого). После этого ранг узла с ключом
. Его потомков тоже
необходимо поменять местами (так как ранг левого сына меньше ранга
правого). После этого ранг узла с ключом  вычисляется как ранг
правого сына плюс
вычисляется как ранг
правого сына плюс  , то есть
, то есть  . Получается куча,
представленная
на рис. 5.18.
. Получается куча,
представленная
на рис. 5.18.