|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Разделенные множества
Представление разделенных множеств древовидной структурой
Пусть, по-прежнему,  — множество, из
элементов которого будет строиться коллекция. Каждое подмножество
коллекции представляется корневым деревом, узлы которого являются
элементами этого подмножества, то есть отождествляются с номерами из
множества
— множество, из
элементов которого будет строиться коллекция. Каждое подмножество
коллекции представляется корневым деревом, узлы которого являются
элементами этого подмножества, то есть отождествляются с номерами из
множества 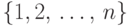 . Корень дерева используется в качестве
имени соответствующего подмножества (канонический элемент). Для каждого
узла дерева определяется узел
. Корень дерева используется в качестве
имени соответствующего подмножества (канонический элемент). Для каждого
узла дерева определяется узел  , являющийся его родителем
в дереве; если
, являющийся его родителем
в дереве; если  — корень, то полагаем
— корень, то полагаем  .
.
Фактически в памяти компьютера это дерево будем представлять
массивом ![p[1\ldots n]](/sites/default/files/tex_cache/32dbcbac54fce8ac8d671a990b801050.png) так, что
так, что  будет предком
узла
будет предком
узла  , если
, если  не является корнем, и
не является корнем, и 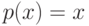 ,
если
,
если  — корень. Если же
— корень. Если же  не входит ни в одно
из подмножеств коллекции, то
не входит ни в одно
из подмножеств коллекции, то 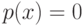 .
.
Рассмотрим пример. Пусть  и коллекция
состоит из двух подмножеств
и коллекция
состоит из двух подмножеств 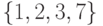 и
и 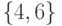 . Деревья,
представляющие эти подмножества, могут быть такими, как на рис.3.1.
Кружочки обозначают узлы дерева; указатели на родителей представлены при помощи стрелок. Именем
одного из этих подмножеств является 3, другого — 6:
. Деревья,
представляющие эти подмножества, могут быть такими, как на рис.3.1.
Кружочки обозначают узлы дерева; указатели на родителей представлены при помощи стрелок. Именем
одного из этих подмножеств является 3, другого — 6:
Реализация операций с помощью древовидной структуры
Операция СОЗДАТЬ
(  ) назначает в качестве родителя
узла
) назначает в качестве родителя
узла  сам узел
сам узел  с помощью присваивания
с помощью присваивания ![p[x]
:= x](/sites/default/files/tex_cache/1b1f2b9e550a9012898dd4208b775ee1.png) .
Таким образом, время выполнения операции есть
.
Таким образом, время выполнения операции есть  .
В результате выполнения операции СОЗДАТЬ(
.
В результате выполнения операции СОЗДАТЬ(  ) образуется новое
одновершинное дерево с петлей в корне, изображенное на
рис. 3.2.
) образуется новое
одновершинное дерево с петлей в корне, изображенное на
рис. 3.2.
Если к коллекции подмножеств, изображенных на рис. 3.1, применить операцию СОЗДАТЬ (5), то получим коллекцию, изображенную на рис. 3.3.
Операция ОБЪЕДИНИТЬ
( 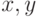 ) назначает узел
) назначает узел  родителем узла
родителем узла  с помощью присваивания
с помощью присваивания ![p[x]:= y](/sites/default/files/tex_cache/958c1a3d3b27c6dccb69ca17b78fbefb.png) .
Заметим, что
.
Заметим, что  и
и  должны быть до выполнения
рассматриваемой операции корнями соответствующих деревьев. Именем вновь образованного
подмножества будет
должны быть до выполнения
рассматриваемой операции корнями соответствующих деревьев. Именем вновь образованного
подмножества будет  , а
, а  перестанет быть именем
какого-либо множества. Время выполнения этой операции есть
перестанет быть именем
какого-либо множества. Время выполнения этой операции есть  .
.
Если применить операцию ОБЪЕДИНИТЬ 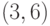 к коллекции,
представленной на рис. 3.3, то получим коллекцию, состоящую из двух
подмножеств
к коллекции,
представленной на рис. 3.3, то получим коллекцию, состоящую из двух
подмножеств 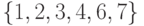 и
и 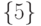 , —
изображенную на рис. 3.4. Именем первого из этих подмножеств
будет 6, второго — 5.
, —
изображенную на рис. 3.4. Именем первого из этих подмножеств
будет 6, второго — 5.
Операция НАЙТИ ( 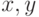 ) осуществляется продвижением по
указателям на родителей от узла
) осуществляется продвижением по
указателям на родителей от узла  до корня дерева.
В качестве
до корня дерева.
В качестве  берется этот корень.
Описанные действия можно реализовать с помощью операторов
берется этот корень.
Описанные действия можно реализовать с помощью операторов
![\formula{
\t \while\ p[x] \ne x\ \t \do\ x := p[x];\ y := x;
}](/sites/default/files/tex_cache/f061d61a83aca4fdf1dcbb5944f0b746.png)
Очевидно, что время выполнения данной операции есть 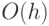 ,
где
,
где  — длина пути из узла
— длина пути из узла  в корень
соответствующего дерева.
Но заметим, что при выполнении операций СОЗДАТЬ и ОБЪЕДИНИТЬ возможно
образование дерева в виде линейной цепочки из
в корень
соответствующего дерева.
Но заметим, что при выполнении операций СОЗДАТЬ и ОБЪЕДИНИТЬ возможно
образование дерева в виде линейной цепочки из  узлов,
изображенной
на рис. 3.5.
узлов,
изображенной
на рис. 3.5.
К такой цепочке может привести, например, следующая последовательность операций
СОЗДАТЬ ( 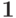 );
);
СОЗДАТЬ (  );
);



СОЗДАТЬ ( 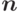 );
);
ОБЪЕДИНИТЬ ( 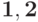 );
);
ОБЪЕДИНИТЬ (  );
);



ОБЪЕДИНИТЬ ( 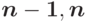 );
);
Как видим,  может достигать величины
может достигать величины  , поэтому
трудоемкость операции НАЙТИ является величиной
, поэтому
трудоемкость операции НАЙТИ является величиной  .
.
Худший случай применения операции НАЙТИ в данной ситуации — это
НАЙТИ (  ). В этом случае необходимо сделать
). В этом случае необходимо сделать 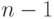 переход по ссылкам
на родителей, чтобы дойти от узла
переход по ссылкам
на родителей, чтобы дойти от узла  к корню дерева
к корню дерева  ,
и один переход, чтобы узнать, что родитель узла
,
и один переход, чтобы узнать, что родитель узла  есть сам
узел
есть сам
узел  .
.
Если операция СОЗДАТЬ выполняется  раз, то время выполнения
последовательности, составленной из
раз, то время выполнения
последовательности, составленной из  операций ОБЪЕДИНИТЬ
и/или НАЙТИ, при рассматриваемой реализации разделенных множеств есть
величина
операций ОБЪЕДИНИТЬ
и/или НАЙТИ, при рассматриваемой реализации разделенных множеств есть
величина  . Действительно, время
выполнения
. Действительно, время
выполнения  операций
ОБЪЕДИНИТЬ, очевидно, есть
операций
ОБЪЕДИНИТЬ, очевидно, есть  , так как время выполнения
одной такой операции есть константа. Время выполнения
, так как время выполнения
одной такой операции есть константа. Время выполнения  операций
НАЙТИ есть
операций
НАЙТИ есть  , так как время выполнения одной такой
операции есть
, так как время выполнения одной такой
операции есть  . Итак, время
выполнения
. Итак, время
выполнения  произвольных операций есть
произвольных операций есть 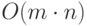 .
.





