| Россия, Пошатово |
Переменные, выражения, присваивания
1.2.27.
(Двоичный поиск) Дана последовательность ![x[1]\le\ldots\le x[n]](/sites/default/files/tex_cache/42f65b653e005ed252c1f0dc1ed123d7.png) целых чисел
и число a.
Выяснить, содержится ли a в этой последовательности, то
есть существует ли i из 1..n, для которого
целых чисел
и число a.
Выяснить, содержится ли a в этой последовательности, то
есть существует ли i из 1..n, для которого ![x[i]=a](/sites/default/files/tex_cache/77e6f47d50c31837b7ca1361c224d001.png) . (Количество действий порядка
. (Количество действий порядка  .)
.)
Решение.
(Предполагаем, что  .)
.)
l := 1; r := n+1;
{r > l, если a есть вообще, то есть и среди x[l]..x[r-1]}
while r - l <> 1 do begin
| m := l + (r-l) div 2 ;
| {l < m < r }
| if x[m] <= a then begin
| | l := m;
| end else begin {x[m] > a}
| | r := m;
| end;
end;(Обратите внимание, что и в случае ![x[m] = a](/sites/default/files/tex_cache/113e580e2abc8d862edf02ca2dab02b3.png) инвариант не нарушается.)
инвариант не нарушается.)
Каждый раз  уменьшается примерно вдвое, откуда
и вытекает требуемая оценка числа действий.
уменьшается примерно вдвое, откуда
и вытекает требуемая оценка числа действий.
Замечание.
В этой задаче существенно, что массив упорядочен - поиск в неупорядоченном массиве требует времени, пропорционального длине массива. (Чтобы убедиться, что какого-то числа нет в массиве, надо просмотреть все его элементы.)
1.2.28. (Из книги Д. Гриса) Имеется массив x: array[1..n] of array[1..m] of integer, упорядоченный по строкам и по столбцам:
![x[i][j] \le x[i][j+1],\\
x[i][j] \le x[i+1][j],](/sites/default/files/tex_cache/023cd31721be4bb8122415e72129aa77.png)
Решение. Представляя себе массив x как матрицу
(прямоугольник, заполненный числами), мы выберем
прямоугольник, в котором только и может содержаться a,
и будем его сужать. Прямоугольник этот будет содержать x[i][j] при 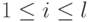 и
и 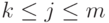
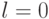 и
и  ).
).l:=n; k:=1;
{l>=0, k<=m+1, если a есть, то в описанном прямоугольнике}
while (l > 0) and (k < m+1) and (x[l][k] <> a) do begin
| if x[l][k] < a then begin
| | k := k + 1; {левый столбец не содержит a, удаляем его}
| end else begin {x[l][k] > a}
| | l := l - 1; {нижняя строка не содержит a, удаляем ее}
| end;
end;
{x[l][k] = a или прямоугольник пуст }
answer:= (l > 0) and (k < m+1) ;Замечание. Здесь та же ошибка: x[l][k] может оказаться неопределенным. (Ее исправление предоставляется читателю.)
1.2.29.
(Московская олимпиада по программированию) Дан неубывающий
массив положительных целых чисел ![a[1]\le a[2]\le\ldots\le a[n]](/sites/default/files/tex_cache/9572ed5154a7853cf850df71930862f7.png) . Найти наименьшее
целое положительное число, не представимое в виде суммы
нескольких элементов этого массива (каждый элемент массива
может быть использован не более одного раза). Число
действий порядка n.
. Найти наименьшее
целое положительное число, не представимое в виде суммы
нескольких элементов этого массива (каждый элемент массива
может быть использован не более одного раза). Число
действий порядка n.
Решение. Пусть известно, что числа, представимые в виде
суммы элементов ![a[1],\ldots,a[k]](/sites/default/files/tex_cache/8d2c0fe258d7c4cc35512a41e7a3fd93.png) , заполняют
отрезок от 1 до некоторого N. Если
, заполняют
отрезок от 1 до некоторого N. Если ![a[k+1] >
N+1](/sites/default/files/tex_cache/0b3db7d628184fb819724212b47eb0ea.png) , то
, то 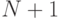 и будет минимальным числом, не
представимым в виде суммы элементов массива
и будет минимальным числом, не
представимым в виде суммы элементов массива ![a[1]\ldots a[n]](/sites/default/files/tex_cache/746f0de843932ec15edd671a9dd7b4ec.png) . Если же
. Если же ![a[k+1]\le N+1](/sites/default/files/tex_cache/82e88935ed8e962aebdf7041fdf9297d.png) ,
то числа, представимые в виде суммы элементов
,
то числа, представимые в виде суммы элементов ![a[1]\ldots a[k+1]](/sites/default/files/tex_cache/9c340ca16df85ade4c1b696d8d0bb1f5.png) , заполняют отрезок от 1 до N+a[k+1].
, заполняют отрезок от 1 до N+a[k+1].
k := 0; N := 0;
{инвариант: числа, представимые в виде суммы элементов
массива a[1]..a[k], заполняют отрезок 1..N}
while (k <> n) and (a[k+1] <= N+1) do begin
| N := N + a[k+1];
| k := k + 1;
end;
{(k = n) или (a[k+1] > N+1); в обоих случаях ответ N+1}
writeln (N+1);(Снова тот же дефект: в условии цикла при ложном первом условии второе не определено.)
1.2.30.
(Для знакомых с основами алгебры) В целочисленном массиве ![a[1]\ldots a[n]](/sites/default/files/tex_cache/746f0de843932ec15edd671a9dd7b4ec.png) хранится перестановка чисел
хранится перестановка чисел 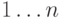 (каждое из чисел встречается по одному
разу).
(каждое из чисел встречается по одному
разу).
(а) Определить четность перестановки. (И в (а), и в (б)
количество действий порядка  .)
.)
(б) Не используя других массивов, заменить перестановку на
обратную (если до работы программы ![a[i]=j](/sites/default/files/tex_cache/ad2828c774d13ecf88dc0a452408fe84.png) , то
после должно быть
, то
после должно быть ![a[j]=i](/sites/default/files/tex_cache/2a4a219ac4940e023553138f958d8f8b.png) ).
).
Указание. (а) Четность перестановки определяется количеством циклов. Чтобы отличать уже пройденные циклы, у их элементов можно, например, менять знак. (б) Обращение производим по циклам.
1.2.31. Дан массив a[1..n] и число b. Переставить числа в массиве таким образом, чтобы слева от некоторой границы стояли числа, меньшие или равные b, а справа от границы - большие или равные b. Число действий порядка n.
Решение.
l:=0; r:=n;
{инвариант: a[1]..a[l]<=b; a[r+1]..a[n]>=b}
while l <> r do begin
| if a[l+1] <= b then begin
| | l:=l+1;
| end else if a[r] >=b then begin
| | r:=r-1;
| end else begin {a[l+1]>b; a[r]<b}
| | ..поменять a[l+1] и a[r]
| | l:=l+1; r:=r-1;
| end;
end;1.2.32. Та же задача, но требуется, чтобы сначала шли элементы, меньшие b, затем равные b, а лишь затем большие b.
Решение. Теперь потребуются три границы: до первой будут идти элементы, меньшие b, от первой до второй - равные b, затем неизвестно какие до третьей, а после третьей - большие b. (Более симметричное решение использовало бы четыре границы, но вряд ли игра стоит свеч.) В качестве очередного рассматриваемого элемента берем элемент справа от средней границы.
l:=0; m:=0; r:=n;
{инвариант: a[1..l]<b; a[l+1..m]=b; a[r+1]..a[n]>b}
while m <> r do begin
| if a[m+1]=b then begin
| | m:=m+1;
| end else if a[m+1] > b then begin
| | ..обменять a[m+1] и a[r]
| | r:=r-1;
| end else begin {a[m+1] < b}
| | ..обменять a[m+1] и a[l+1]
| | l:=l+1; m:=m+1;
| end;
end;1.2.33. (Вариант предыдущей задачи, названный в книге Дейкстры задачей о голландском флаге.) В массиве длины n стоят числа 0, 1 и 2. Переставить их в порядке возрастания, если единственной разрешенной операцией (помимо чтения) над массивом является перестановка двух элементов. Число действий порядка n.
1.2.34.
Дан массив a[1..n] и число  . Для
каждого участка из m стоящих рядом членов (таких
участков, очевидно,
. Для
каждого участка из m стоящих рядом членов (таких
участков, очевидно,  ) вычислить его
сумму. Общее число действий должно быть порядка n.
) вычислить его
сумму. Общее число действий должно быть порядка n.
Решение. Переходя от участка к соседнему, мы добавляем один член, а другой вычитаем.
1.2.35.
Дана квадратная таблица a[1..n][1..n] и число  . Для каждого квадрата
. Для каждого квадрата 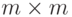 в этой таблице вычислить сумму стоящих в нем чисел. Общее
число действий порядка
в этой таблице вычислить сумму стоящих в нем чисел. Общее
число действий порядка 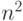 .
.
Решение. Сначала для каждого горизонтального
прямоугольника размером 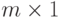 вычисляем сумму
стоящих в нем чисел. (При сдвиге такого прямоугольника по
горизонтали на 1 нужно добавить одно число и одно
вычесть.) Затем, используя эти суммы, вычисляем суммы
в квадратах. (При сдвиге квадрата по вертикали добавляется
полоска, а другая полоска убавляется.)
вычисляем сумму
стоящих в нем чисел. (При сдвиге такого прямоугольника по
горизонтали на 1 нужно добавить одно число и одно
вычесть.) Затем, используя эти суммы, вычисляем суммы
в квадратах. (При сдвиге квадрата по вертикали добавляется
полоска, а другая полоска убавляется.)
1.2.36.
В массиве ![a[1]\ldots a[n]](/sites/default/files/tex_cache/746f0de843932ec15edd671a9dd7b4ec.png) встречаются по одному
разу все целые числа от 0 до n, кроме одного. Найти
пропущенное число за время порядка n и с конечной
дополнительной памятью.
встречаются по одному
разу все целые числа от 0 до n, кроме одного. Найти
пропущенное число за время порядка n и с конечной
дополнительной памятью.
Указание. Сложить все числа в массиве.

