Переменные, выражения, присваивания

1.1.7. Дано натуральное (целое неотрицательное) число а и целое положительное число d. Вычислить частное q и остаток r при делении а на d, не используя операций div и mod.

Решение. Согласно определению, , .

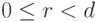{a >= 0; d > 0} 
r := a; q := 0; 
{инвариант: a = q * d + r, 0 <= r} 
while not (r < d) do begin 
| {r >= d} 
| r := r - d; {r >= 0} 
| q := q + 1; 
end;

1.1.8.Дано натуральное , вычислить ! ( , !).

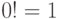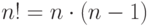1.1.9.Последовательность Фибоначчи определяется так: 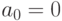, , 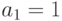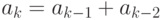при . Дано , вычислить .

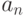1.1.10. Та же задача, если требуется, чтобы число операций было пропорционально . (Переменные должны быть целочисленными.)

Указание. Пара соседних чисел Фибоначчи получается из предыдущей умножением на матрицу

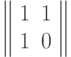
- так что задача сводится к возведению матрицы в степень . Это можно сделать за действий тем же способом, что и для чисел.

1.1.11. Дано натуральное n, вычислить

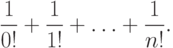
1.1.12. То же, если требуется, чтобы количество операций (выполненных команд присваивания) было бы порядка (не более для некоторой константы ).

Решение. Инвариант: 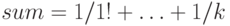!, ! (важно не вычислять заново каждый раз !).

1.1.13.Даны два натуральных числа a и b, не равные нулю одновременно. Вычислить НОД(a,b) - наибольший общий делитель а и b.

Решение. Вариант 1.

if a > b then begin 
| k := a; 
end else begin 
| k := b; 
end; 
{k = max (a,b)} 
{инвариант: никакое  число, большее k, не является 
  общим делителем} 
while not ((a mod k = 0) and (b mod k = 0)) do begin 
| k := k - 1; 
end; 
{k - общий делитель, большие - нет}

Вариант 2 (алгоритм Евклида). Будем считать, что НОД(0,0)=0. Тогда НОД(a,b) =НОД(a-b,b) = НОД(a,b-a) ; НОД(a,0) =НОД(0,a) = a для всех .

m := a; n := b; 
{инвариант: НОД (a,b) = НОД (m,n); m,n >= 0 } 
while not ((m=0) or (n=0)) do begin 
| if m >= n then begin 
| | m := m - n; 
| end else begin 
| | n := n - m; 
| end; 
end; 
{m = 0 или n = 0} 
if m = 0 then begin 
| k := n; 
end else begin {n = 0} 
| k := m; 
end;

1.1.14.Написать модифицированный вариант алгоритма Евклида, использующий соотношения НОД(a,b) = НОД(a mod b, b) при , НОД(a,b) = НОД(a, b mod a) при .