| Россия, Пошатово |
Переменные, выражения, присваивания
1.1.20.Составить программу, печатающую квадраты всех натуральных чисел от 0 до заданного натурального n.
Решение.
k:=0;
writeln (k*k);
{инвариант: k<=n, напечатаны все
квадраты до k включительно}
while not (k=n) do begin
| k:=k+1;
| writeln (k*k);
end;1.1.21. Та же задача, но разрешается использовать из арифметических операций лишь сложение и вычитание, причем общее число действий должно быть порядка n.
Решение. Введем переменную k_square (square -
квадрат), связанную с k соотношением 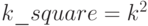 :
:
k := 0; k_square := 0;
writeln (k_square);
while not (k = n) do begin
| k := k + 1;
| {k_square = (k-1) * (k-1) = k*k - 2*k + 1}
| k_square := k_square + k + k - 1;
| writeln (k_square);
end;Замечание. Можно обойтись без вычитания с помощью такой хитрости:
while not (k = n) do begin
| k_square := k_square + k;
| {k_square = k*k + k}
| k := k + 1;
| {k_square = (k-1)*(k-1)+(k-1)=k*k-k}
| k_square := k_square + k;
end;1.1.22.
Составить программу, печатающую разложение на простые
множители заданного натурального числа  (другими словами, требуется печатать только простые числа
и произведение напечатанных чисел должно быть равно n ;
если
(другими словами, требуется печатать только простые числа
и произведение напечатанных чисел должно быть равно n ;
если 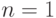 , печатать ничего не надо).
, печатать ничего не надо).
Решение. Вариант 1.
k := n;
{инвариант: произведение напечатанных чисел и k равно
n, напечатаны только простые числа}
while not (k = 1) do begin
| l := 2;
| {инвариант: k не имеет делителей в интервале (1,l)}
| while k mod l <> 0 do begin
| | l := l + 1;
| end;
| {l - наименьший делитель k, больший 1, следовательно,
| простой}
| writeln (l);
| k:=k div l;
end;Вариант 2.
k := n; l := 2;
{произведение k и напечатанных чисел равно n; напечатанные
числа просты; k не имеет делителей, меньших l}
while not (k = 1) do begin
| if k mod l = 0 then begin
| | {k делится на l и не имеет делителей,
| | меньших l, значит, l просто}
| | k := k div l;
| | writeln (l);
| end else begin
| | { k не делится на l }
| | l := l+1;
| end;
end;1.1.23. Составить программу решения предыдущей задачи, использующую тот факт, что составное число имеет делитель, не превосходящий квадратного корня из этого числа.
Решение. Во втором варианте решения вместо l:=l+1 можно написать
if l*l > k then begin | l:=k; end else begin | l:=l+1; end;
1.1.24.
Проверить, является ли заданное натуральное число  простым.
простым.
1.1.25.
(Для знакомых с основами алгебры) Дано целое гауссово число 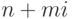 (принадлежащее
(принадлежащее ![\mathbb{Z}[i]](/sites/default/files/tex_cache/89d7b73007774eb3de166a86b7686ac6.png) ).
).
(a) Проверить, является ли оно простым (в ![\mathbb{Z}[i]](/sites/default/files/tex_cache/89d7b73007774eb3de166a86b7686ac6.png) ).
).
(б) Напечатать его разложение на простые (в ![\mathbb{Z}[i]](/sites/default/files/tex_cache/89d7b73007774eb3de166a86b7686ac6.png) )
множители.
)
множители.
1.1.26.Разрешим применять команды write(i) лишь при 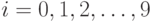 . Составить
программу, печатающую десятичную запись заданного
натурального числа
. Составить
программу, печатающую десятичную запись заданного
натурального числа  . (Случай
. (Случай 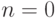 явился бы некоторым исключением, так как обычно нули
в начале числа не печатаются, а для
явился бы некоторым исключением, так как обычно нули
в начале числа не печатаются, а для 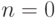 -
печатаются.)
-
печатаются.)
Решение.
base:=1;
{base - степень 10, не превосходящая n}
while 10 * base <= n do begin
| base:= base * 10;
end;
{base - максимальная степень 10, не превосходящая n}
k:=n;
{инвариант: осталось напечатать k с тем же числом
знаков, что в base; base = 100..00}
while base <> 1 do begin
| write(k div base);
| k:= k mod base;
| base:= base div 10;
end;
{base=1; осталось напечатать однозначное число k}
write(k);Типичная ошибка при решении этой задачи: неправильно
обрабатываются числа с нулями посередине. Приведенный
инвариант допускает случай, когда 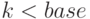 ; в этом
случае печатание k начинается со старших нулей.
; в этом
случае печатание k начинается со старших нулей.
