| Россия, Пошатово |
Переменные, выражения, присваивания
1.2.20.
Даны два массива ![x[1]\le\ldots\le x[k]](/sites/default/files/tex_cache/14615d82980fe668134f043eeed998ea.png) и
и ![y[1]\le\ldots\le y[l]](/sites/default/files/tex_cache/acbad681e5a03a184841474c97c83156.png) . "Соединить" их
в массив
. "Соединить" их
в массив ![z[1]\le\ldots\le z[m]](/sites/default/files/tex_cache/027fa1df8108911be4e7c923afda1800.png) (
( 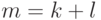 ; каждый элемент должен входить
в массив z столько раз, сколько раз он входит в общей
сложности в массивы x и y ). Число действий
порядка m.
; каждый элемент должен входить
в массив z столько раз, сколько раз он входит в общей
сложности в массивы x и y ). Число действий
порядка m.
Решение.
k1 := 0; l1 := 0;
{инвариант: ответ получится, если к z[1]..z[k1+l1] добавить
справа соединение массивов x[k1+1]..x[k] и y[l1+1]..y[l]}
while (k1 <> k) or (l1 <> l) do begin
| if k1 = k then begin
| | {l1 < l}
| | l1 := l1 + 1;
| | z[k1+l1] := y[l1];
| end else if l1 = l then begin
| | {k1 < k}
| | k1 := k1 + 1;
| | z[k1+l1] := x[k1];
| end else if x[k1+1] <= y[l1+1] then begin
| | k1 := k1 + 1;
| | z[k1+l1] := x[k1];
| end else if x[k1+1] >= y[l1+1] then begin
| | l1 := l1 + 1;
| | z[k1+l1] := y[l1];
| end else begin
| | { такого не бывает }
| end;
end;
{k1 = k, l1 = l, массивы соединены}Этот процесс можно пояснить так. Пусть у нас есть две стопки карточек, отсортированных по алфавиту. Мы соединяем их в одну стопку, выбирая каждый раз ту из верхних карточек обеих стопок, которая идет раньше в алфавитном порядке. Если в одной стопке карточки кончились, берем их из другой стопки.
1.2.21.
Даны два массива ![x[1]\le\ldots\le x[k]](/sites/default/files/tex_cache/14615d82980fe668134f043eeed998ea.png) и
и ![y[1]\le\ldots\le y[l]](/sites/default/files/tex_cache/acbad681e5a03a184841474c97c83156.png) . Найти их "
пересечение", то есть массив
. Найти их "
пересечение", то есть массив ![z[1]\le\ldots\le z[m],](/sites/default/files/tex_cache/935b3ff5c71b9cd7ee03b09745213b24.png) содержащий их общие
элементы, причем кратность каждого элемента в массиве z
равняется минимуму из его кратностей в массивах x
и y. Число действий порядка
содержащий их общие
элементы, причем кратность каждого элемента в массиве z
равняется минимуму из его кратностей в массивах x
и y. Число действий порядка  .
.
1.2.22.
Даны два массива ![x[1]\le\ldots\le x[k]](/sites/default/files/tex_cache/14615d82980fe668134f043eeed998ea.png) и
и ![y[1]\le\ldots\le y[l]](/sites/default/files/tex_cache/acbad681e5a03a184841474c97c83156.png) и число q. Найти сумму
вида
и число q. Найти сумму
вида ![x[i]+y[j]](/sites/default/files/tex_cache/d63a4c921b9ea76c7057c8eab5a96f14.png) , наиболее близкую к числу q.
(Число действий порядка k+l, дополнительная память -
фиксированное число целых переменных, сами массивы
менять не разрешается.)
, наиболее близкую к числу q.
(Число действий порядка k+l, дополнительная память -
фиксированное число целых переменных, сами массивы
менять не разрешается.)
Указание.
Надо найти минимальное расстояние между элементами ![x[1]\le\ldots\le x[k]](/sites/default/files/tex_cache/14615d82980fe668134f043eeed998ea.png) и
и ![q-y[l]\le\ldots\le q-y[1]](/sites/default/files/tex_cache/270b695cd723083d9c2ad07506e85b49.png) , что нетрудно
сделать в ходе их слияния в один (воображаемый) массив.
, что нетрудно
сделать в ходе их слияния в один (воображаемый) массив.
1.2.23.
(из книги Д. Гриса) Некоторое число содержится в каждом из
трех целочисленных неубывающих массивов ![x[1]\le\ldots\le x[p]](/sites/default/files/tex_cache/51f2aa8ff0ab46e7ba2674ceaa1da91a.png) ,
, ![y[1]\le\ldots\le y[q]](/sites/default/files/tex_cache/4f52f033107405cdbaab9f82779fd629.png) ,
, ![z[1]\le\ldots\le z[r]](/sites/default/files/tex_cache/0fb52313d7aef9b94bdd0d3adc2649f0.png) . Найти одно из таких чисел.
Число действий должно быть порядка
. Найти одно из таких чисел.
Число действий должно быть порядка 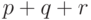 .
.
Решение.
p1:=1; q1=1; r1:=1;
{инвариант: x[p1]..x[p], y[q1]..y[q], z[r1]..z[r]
содержат общий элемент}
while not ((x[p1]=y[q1]) and (y[q1]=z[r1])) do begin
| if x[p1]<y[q1] then begin
| | p1:=p1+1;
| end else if y[q1] <z[r1] then begin
| | q1:=q1+1;
| end else if z[r1] <x[p1] then begin
| | r1:=r1+1;
| end else begin
| | { так не бывает }
| end;
end;
{x[p1] = y[q1] = z[r1]}
writeln (x[p1]);1.2.24. Та же задача, только заранее не известно, существует ли общий элемент в трех неубывающих массивах и требуется это выяснить (и найти один из общих элементов, если они есть).
1.2.25. Элементами массива a[1..n] являются неубывающие массивы [1..m] целых чисел:
![\begin{multiple}
\text{a: array [1..n] \text {of array} [1..m] \text {of integer};}\\
%
\w{a[1][1]}\le\ldots\le\w{a[1][m]},\ldots,
\w{a[n][1]}\le\ldots\le\w{a[n][m]}.
\end{multiple)](/sites/default/files/tex_cache/9f45bec60415c5b89ec7f13277ecbfa0.png)
![a[i][j]=x](/sites/default/files/tex_cache/1393b12aefd70de9f5cecc5936b1de18.png) ). Найти одно из таких чисел х.
). Найти одно из таких чисел х.Решение. Введем массив ![b[1]\ldots b[n]](/sites/default/files/tex_cache/bffde2b90f4a2adb91a126f3b3bb5d4f.png) ,
отмечающий начало "остающейся части" массивов
,
отмечающий начало "остающейся части" массивов ![a[1],\ldots,a[n]](/sites/default/files/tex_cache/741bf95d2f969f1b1f33fa0c96b82f97.png) .
.
for k:=1 to n do begin
| b[k]:=1;
end;
eq := true;
for k := 2 to n do begin
| eq := eq and (a[1][b[1]] = a[k][b[k]]);
end;
{инвариант: оставшиеся части пересекаются, т.е. существует
такое х, что для всякого i из [1..n] найдется j из [1..m],
не меньшее b[i], для которого a[i][j] = х; eq <=> первые
элементы оставшихся частей равны}
while not eq do begin
| s := 1; k := 1;
| {a[s][b[s]] - минимальное среди a[1][b[1]]..a[k][b[k]]}
| while k <> n do begin
| | k := k + 1;
| | if a[k][b[k]] < a[s][b[s]] then begin
| | | s := k;
| | end;
| end;
| {a[s][b[s]] - минимальное среди a[1][b[1]]..a[n][b[n]]}
| b [s] := b [s] + 1;
| for k := 2 to n do begin
| | eq := eq and (a[1][b[1]] = a[k][b[k]]);
| end;
end;
writeln (a[1][b[1]]);1.2.26.
Приведенное решение предыдущей задачи требует порядка  действий. Придумать способ с числом действий
порядка mn.
действий. Придумать способ с числом действий
порядка mn.
Указание. Придется пожертвовать симметрией и выбрать одну из строк за основную. Двигаясь по основной строке, поддерживаем такое соотношение: во всех остальных строках отмечен максимальный элемент, не превосходящий текущего элемента основной строки.
