| Россия, Пошатово |
Переменные, выражения, присваивания
1.2.10. Дан массив x[1]..x[n] целых чисел. Не используя других массивов, переставить элементы массива в обратном порядке.
Решение. Элементы x[i] и x[n+1-i] нужно поменять
местами для всех i, для которых  , то есть
, то есть
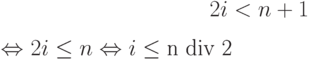
for i := 1 to n div 2 do begin | ...поменять местами x[i] и x[n+1-i]; end;
1.2.11.
(Из книги Д. Гриса) Дан массив целых чисел x[1]..x[m+n], рассматриваемый как соединение двух его
отрезков: начала x[1]..x[m] длины m и конца x[m+1]..x[m+n] длины n. Не используя дополнительных
массивов, переставить начало и конец.
(Число действий порядка 
Решение. Вариант 1. Перевернем (расположим в обратном порядке) отдельно начало и конец массива, а затем перевернем весь массив как единое целое.
Вариант 2. (А. Г. Кушниренко) Рассматривая массив записанным по кругу, видим, что требуемое действие - поворот круга. Как известно, поворот есть композиция двух осевых симметрий.
Вариант 3. Рассмотрим более общую задачу - обмен двух
участков массива x[p+1]..x[q] и x[q+1]..x[r].
Предположим, что длина левого участка (назовем его  ) не
больше длины правого (назовем его
) не
больше длины правого (назовем его  ). Выделим
в
). Выделим
в  начало той же длины, что и
начало той же длины, что и  , назовем его
, назовем его 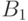 ,
а остаток
,
а остаток 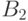 . (Так что
. (Так что  , если обозначать
плюсом приписывание массивов друг к другу.) Нам надо из
, если обозначать
плюсом приписывание массивов друг к другу.) Нам надо из 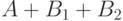 получить
получить 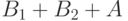 . Меняя местами
участки
. Меняя местами
участки  и
и 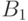 - они имеют одинаковую длину, и сделать это
легко, - получаем
- они имеют одинаковую длину, и сделать это
легко, - получаем 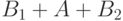 , и осталось поменять
местами
, и осталось поменять
местами  и
и 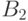 . Тем самым мы свели дело
к перестановке
двух отрезков меньшей длины. Итак, получаем такую схему
программы:
. Тем самым мы свели дело
к перестановке
двух отрезков меньшей длины. Итак, получаем такую схему
программы:
p := 0; q := m; r := m + n;
{инвариант: осталось переставить x[p+1..q], x[q+1..r]}
while (p <> q) and (q <> r) do begin
| {оба участка непусты}
| if (q - p) <= (r - q) then begin
| | ..переставить x[p+1]..x[q] и x[q+1]..x[q+(q-p)]
| | pnew := q; qnew := q + (q - p);
| | p := pnew; q := qnew;
| end else begin
| | ..переставить x[q-(r-q)+1]..x[q] и x[q+1]..x[r]
| | qnew := q - (r - q); rnew := q;
| | q := qnew; r := rnew;
| end;
end;Оценка времени работы: на очередном шаге оставшийся для
обработки участок становится короче на длину  ; число
действий при этом также пропорционально длине
; число
действий при этом также пропорционально длине  .
.
1.2.12.Коэффициенты многочлена лежат в массиве a: array[0..n]
of integer ( n - натуральное число, степень
многочлена). Вычислить значение этого многочлена
в точке x, то есть ![a[n]\,x^n+\ldots+a[1]\,x+a[0]](/sites/default/files/tex_cache/370d3caffbd2fda34ea08773c085444a.png) .
.
Решение. (Описываемый алгоритм называется схемой Горнера.)
k := 0; y := a[n];
{инвариант: 0 <= k <= n,
y= a[n]*(x в степени k)+...+a[n-1]*(x в степени k-1)+...+
+ a[n-k]*(x в степени 0)}
while k<>n do begin
| k := k + 1;
| y := y * x + a [n-k];
end;1.2.13. (Для знакомых с основами анализа; сообщил А. Г. Кушниренко) Дополнить алгоритм вычисления значения многочлена в заданной точке по схеме Горнера вычислением значения его производной в той же точке.
Решение. Добавление нового коэффициента соответствует
переходу от многочлена  к многочлену
к многочлену 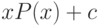 . Его производная в точке
. Его производная в точке  равна
равна 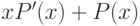 . (Это
решение обладает забавным свойством: не надо знать заранее степень
многочлена. Если требовать выполнения этого условия, да еще
просить вычислять только значение производной, не упоминая
о самом многочлене, получается не такая уж простая задача.)
. (Это
решение обладает забавным свойством: не надо знать заранее степень
многочлена. Если требовать выполнения этого условия, да еще
просить вычислять только значение производной, не упоминая
о самом многочлене, получается не такая уж простая задача.)
Общее утверждение о сложности вычисления производных таково:
1.2.14.
(В. Баур, Ф. Штрассен)
Дана программа вычисления значения некоторого многочлена 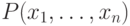 , содержащая только команды
присваивания. Их правые части - выражения, содержащие
сложение, умножение, константы, переменные
, содержащая только команды
присваивания. Их правые части - выражения, содержащие
сложение, умножение, константы, переменные 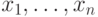 и ранее встречавшиеся (в левой части) переменные. Доказать,
что существует программа того же типа, вычисляющая все
и ранее встречавшиеся (в левой части) переменные. Доказать,
что существует программа того же типа, вычисляющая все  производных
производных 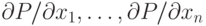 ,
причем общее число арифметических операций не более чем
в
,
причем общее число арифметических операций не более чем
в  раз превосходит число арифметических операций
в исходной программе. Константа
раз превосходит число арифметических операций
в исходной программе. Константа  не зависит от
не зависит от  .
.
Указание. Можно считать, что каждая команда - сложение двух чисел, умножение двух чисел или умножение на константу. Использовать индукцию по числу команд, применяя индуктивное предположение к программе, получающейся отбрасыванием первой команды.
1.2.15.В массивах a: array[0..k] of integer и b:
array[0..l] of integer хранятся коэффициенты двух
многочленов степеней k и l. Поместить в массив c: array[0..m] of integer коэффициенты их
произведения. (Числа 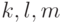 - натуральные,
- натуральные, 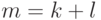 ; элемент массива с индексом i
содержит коэффициент при степени i.)
; элемент массива с индексом i
содержит коэффициент при степени i.)
Решение.
for i:=0 to m do begin | c[i]:=0; end; for i:=0 to k do begin | for j:=0 to l do begin | | c[i+j] := c[i+j] + a[i]*b[j]; | end; end;
1.2.16.
Предложенный выше алгоритм перемножения многочленов требует
порядка 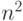 действий для перемножения двух многочленов
степени
действий для перемножения двух многочленов
степени  . Придумать более эффективный (для
больших
. Придумать более эффективный (для
больших  )
алгоритм, которому достаточно порядка
)
алгоритм, которому достаточно порядка 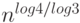 действий.
действий.
Указание.
Представим себе, что надо перемножить два многочлена
степени 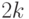 . Их можно представить в виде
. Их можно представить в виде
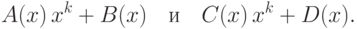

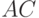 ,
,  ,
, 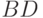 требует
четырех умножений многочленов степени
требует
четырех умножений многочленов степени  , однако их
количество можно сократить до трех с помощью такой
хитрости: вычислить
, однако их
количество можно сократить до трех с помощью такой
хитрости: вычислить 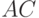 ,
, 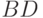 и
и 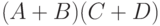 , а затем
заметить, что
, а затем
заметить, что 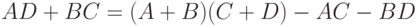 .
.1.2.17.Даны два возрастающих массива x: array[1..k] of
integer и y: array[1..l] of integer. Найти
количество общих элементов в этих массивах, то есть
количество тех целых t, для которых ![t = x[i] =
y[j]](/sites/default/files/tex_cache/bfa7401043e48dad2ae02f3da8e064a5.png) для некоторых i и j. (Число действий
порядка
для некоторых i и j. (Число действий
порядка  .)
.)
Решение.
k1:=0; l1:=0; n:=0;
{инвариант: 0<=k1<=k; 0<=l1<=l;
искомый ответ = n + количество общих
элементов в x[k1+1]...x[k] и y[l1+1]...y[l]}
while (k1 <> k) and (l1 <> l) do begin
| if x[k1+1] < y[l1+1] then begin
| | k1 := k1 + 1;
| end else if x[k1+1] > y[l1+1] then begin
| | l1 := l1 + 1;
| end else begin {x[k1+1] = y[l1+1]}
| | k1 := k1 + 1;
| | l1 := l1 + 1;
| | n := n + 1;
| end;
end;
{k1 = k или l1 = l, поэтому одно из множеств, упомянутых
в инварианте, пусто, а n равно искомому ответу}Замечание. В третьей альтернативе достаточно было бы увеличивать одну из переменных k1, l1 ; вторая добавлена для симметрии.
1.2.18.Решить предыдущую задачу, если про массивы известно лишь,
что ![x[1]\le\ldots\le x[k]](/sites/default/files/tex_cache/14615d82980fe668134f043eeed998ea.png) и
и ![y[1]\le\ldots\le y[l]](/sites/default/files/tex_cache/acbad681e5a03a184841474c97c83156.png) (возрастание заменено
неубыванием).
(возрастание заменено
неубыванием).
Решение. Условие возрастания было использовано в третьей
альтернативе выбора: сдвинув k1 и l1 на 1, мы
тем самым уменьшали на 1 количество общих элементов
в ![x[k1+1]\ldots x[k]](/sites/default/files/tex_cache/9d93ebcf270206f0f251ef8101734d52.png) и
и ![x[l1+1]\ldots x[l]](/sites/default/files/tex_cache/1b9ad5749ea9839788f8f6ad9b27534c.png) . Теперь это придется делать
сложнее.
. Теперь это придется делать
сложнее.
...
end else begin {x[k1+1] = y[l1+1]}
| t := x [k1+1];
| while (k1<k) and (x[k1+1]=t) do begin
| | k1 := k1 + 1;
| end;
| while (l1<l) and (x[l1+1]=t) do begin
| | l1 := l1 + 1;
| end;
| n := n + 1;
end;Замечание. Эта программа имеет дефект: при проверке условия
![$$
\w{(k1<k) and (x[k1+1]=t)}
$$](/sites/default/files/tex_cache/ffbe45ee30d6be5fc03c7478555b685b.png)
Но если мы не хотим полагаться на такое свойство используемой нами реализации паскаля (не предусмотренное его автором Н. Виртом), то можно поступить так. Введем дополнительную переменную b: boolean и напишем:
if k1 < k then b := (x[k1+1]=t) else b:=false;
{b = (k1<k) and (x[k1+1] = t)}
while b do begin
| k1:=k1+1;
| if k1 < k then b := (x[k1+1]=t) else b:=false;
end;Можно также сделать иначе:
end else begin {x[k1+1] = y[l1+1]}
| if k1 + 1 = k then begin
| | k1 := k1 + 1;
| | n := n + 1;
| end else if x[k1+1] = x [k1+2] then begin
| | k1 := k1 + 1;
| end else begin
| | k1 := k1 + 1;
| | n := n + 1;
| end;
end;Так будет короче, хотя менее симметрично.
Наконец, можно увеличить размер массива в его описании, включив в него фиктивные элементы.
1.2.19.
Даны два неубывающих массива x: array[1..k] of
integer и y: array[1..l] of integer. Найти
число различных элементов среди ![x[1],\ldots,x[k],y[1],\ldots,y[l]](/sites/default/files/tex_cache/7a628e75454d972aebea1c592b1d43f9.png) . (Число
действий порядка
. (Число
действий порядка  .)
.)
