| Россия, Пошатово |
Переменные, выражения, присваивания
1.1.15.
Даны натуральные a и b, не равные 0
одновременно. Найти d = НОД(a,b) и такие
целые x и y, что 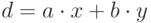 .
.
Решение. Добавим в алгоритм Евклида переменные p, q, r, s и впишем в инвариант условия m = p*a+q*b ; n = r*a+s*b.
m:=a; n:=b; p := 1; q := 0; r := 0; s := 1;
{инвариант: НОД (a,b) = НОД (m,n); m,n >= 0
m = p*a + q*b; n = r*a + s*b.}
while not ((m=0) or (n=0)) do begin
| if m >= n then begin
| | m := m - n; p := p - r; q := q - s;
| end else begin
| | n := n - m; r := r - p; s := s - q;
| end;
end;
if m = 0 then begin
| k :=n; x := r; y := s;
end else begin
| k := m; x := p; y := q;
end;1.1.16.Решить предыдущую задачу, используя в алгоритме Евклида деление с остатком.
1.1.17. (Э. Дейкстра) Добавим в алгоритм Евклида дополнительные переменные u, v, z:
m := a; n := b; u := b; v := a;
{инвариант: НОД (a,b) = НОД (m,n); m,n >= 0 }
while not ((m=0) or (n=0)) do begin
| if m >= n then begin
| | m := m - n; v := v + u;
| end else begin
| | n := n - m; u := u + v;
| end;
end;
if m = 0 then begin
| z:= v;
end else begin {n=0}
| z:= u;
end;Доказать, что после исполнения алгоритма значение z
равно удвоенному наименьшему общему кратному
чисел a, b:  .
.
Решение. Заметим, что величина  не меняется в ходе выполнения алгоритма.
Остается воспользоваться тем, что вначале она равна
не меняется в ходе выполнения алгоритма.
Остается воспользоваться тем, что вначале она равна  и что
и что  .
.
1.1.18. Написать вариант алгоритма Евклида, использующий соотношения
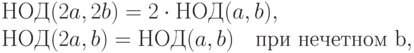
не включающий деления с остатком, а использующий лишь
деление на 2 и проверку четности. (Число действий
должно быть порядка  для исходных данных,
не превосходящих k.)
для исходных данных,
не превосходящих k.)
Решение.
m:= a; n:=b; d:=1;
{НОД(a,b) = d * НОД(m,n)}
while not ((m=0) or (n=0)) do begin
| if (m mod 2 = 0) and (n mod 2 = 0) then begin
| | d:= d*2; m:= m div 2; n:= n div 2;
| end else if (m mod 2 = 0) and (n mod 2 = 1) then begin
| | m:= m div 2;
| end else if(m mod 2 = 1) and (n mod 2 = 0) then begin
| | n:= n div 2;
| end else if (m mod 2=1) and (n mod 2=1) and (m>=n) then begin
| | m:= m-n;
| end else if (m mod 2=1) and (n mod 2=1) and (m<=n) then begin
| | n:= n-m;
| end;
end;
{m=0 => ответ=d*n; n=0 => ответ=d*m}Оценка числа действий: каждое второе действие делит хотя бы одно из чисел m и n пополам.
1.1.19.
Дополнить алгоритм предыдущей задачи поиском x и y, для которых 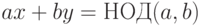 .
.
Решение. (Идея сообщена Д. Звонкиным.) Прежде всего заметим, что одновременное деление a и b пополам не меняет искомых x и y. Поэтому можно считать, что с самого начала одно из чисел a и b нечетно. (Это свойство будет сохраняться и далее.)
Теперь попытаемся, как и раньше, хранить такие числа 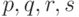 , что
, что
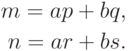
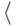 числитель, показатель степени двойки
в знаменателе
числитель, показатель степени двойки
в знаменателе 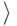 . В итоге мы получаем d в виде
комбинации a и b с двоично-рациональными
коэффициентами. Иными словами, мы имеем
. В итоге мы получаем d в виде
комбинации a и b с двоично-рациональными
коэффициентами. Иными словами, мы имеем
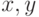 и натурального
и натурального  .
Что делать, если
.
Что делать, если  ? Если x и y четны, то на 2 можно сократить. Если это не так, положение
можно исправить преобразованием
? Если x и y четны, то на 2 можно сократить. Если это не так, положение
можно исправить преобразованием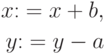
 ). Убедимся в этом.
Напомним, что мы считаем, что одно из чисел a и b
нечетно. Пусть это будет a. Если при этом y четно,
то и x должно быть четным (иначе
). Убедимся в этом.
Напомним, что мы считаем, что одно из чисел a и b
нечетно. Пусть это будет a. Если при этом y четно,
то и x должно быть четным (иначе  будет нечетным). А при
нечетном y вычитание из него нечетного a
делает y четным.
будет нечетным). А при
нечетном y вычитание из него нечетного a
делает y четным.