| Россия, Пошатово |
Разные алгоритмы на графах
9.1. Кратчайшие пути
В этом разделе рассматриваются различные варианты одной
задач. Пусть имеется n городов, пронумерованных числами
от 1 до n. Для каждой пары городов
с номерами i, j в таблице a[i][j] хранится
целое число - цена прямого авиабилета из города i
в город j. Считается, что рейсы существуют между любыми
городами, ![{a[i][i]}={0}](/sites/default/files/tex_cache/941040447065c996e2e32125ee2ec990.png) при всех i, a[i][j]
может отличаться от a[j][i]. Наименьшей стоимостью
проезда из i в j считается минимально возможная
сумма цен билетов для маршрутов (в том числе
с пересадками), ведущих из i в j. (Она не
превосходит a[i][j], но может быть меньше.)
при всех i, a[i][j]
может отличаться от a[j][i]. Наименьшей стоимостью
проезда из i в j считается минимально возможная
сумма цен билетов для маршрутов (в том числе
с пересадками), ведущих из i в j. (Она не
превосходит a[i][j], но может быть меньше.)
В предлагаемых ниже задачах требуется найти наименьшую стоимость проезда для некоторых пар городов при тех или иных ограничениях на массив a и на время работы алгоритма.
9.1.1. Предположим, что не существует замкнутых маршрутов, для которых сумма цен отрицательна. Доказать, что в этом случае маршрут с наименьшей стоимостью существует.
Решение. Маршрут длиной больше n всегда содержит цикл, поэтому минимум можно искать среди маршрутов длиной не более n, а их конечное число.
Во всех следующих задачах предполагается, что это условие (отсутствие циклов с отрицательной суммой) выполнено.
9.1.2.
Найти наименьшую стоимость проезда из 1-го города во
все остальные за время  .
.
Решение. Обозначим через МинСт(1,s,k) наименьшую стоимость проезда из 1 в s менее чем с k пересадками. Тогда выполняется такое соотношение:
![{МинСт}({1},{s},{k+1}) =
min \Bigl({МинСт(1,s,k)},
\min_{i=1..n} {МинСт(1,i,k)}+{a[i]}\!{[s]})\Bigr)](/sites/default/files/tex_cache/071abeecab6431ee55b6a57acd48e27c.png)
 .
.k:= 1;
for i := 1 to n do begin x[i] := a[1][i]; end;
{инвариант: x[i] = МинСт(1,i,k)}
while k <> n do begin
| for s := 1 to n do begin
| | y[s] := x[s];
| | for i := 1 to n do begin
| | | if y[s] > x[i]+a[i][s] then begin
| | | | y[s] := x[i]+a[i][s];
| | | end;
| | end
| | {y[s] = МинСт(1,s,k+1)}
| end;
| for i := 1 to n do begin x[s] := y[s]; end;
| k := k + 1;
end;Приведенный алгоритм называют алгоритмом динамического программирования, или алгоритмом Форда-Беллмана.
9.1.3. Доказать, что программа останется правильной, если не заводить массива y, а производить изменения в самом массиве x (заменив в программе все вхождения буквы y на x и затем удалить ставшие лишними строки).
Решение. Инвариант будет таков:
![{МинСт(1,i,n)} \le {x[i]} \le {МинСт(1,i,k)}.](/sites/default/files/tex_cache/270e93305889fda72507d78839b6da64.png)
Этот алгоритм может быть улучшен в двух отношениях: можно
за то же время  найти наименьшую стоимость
проезда
найти наименьшую стоимость
проезда 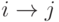 для всех
пар i, j (а не только при
для всех
пар i, j (а не только при 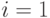 ), а можно
сократить время работы до
), а можно
сократить время работы до  . Правда, в последнем
случае нам потребуется, чтобы все цены a[i][j] были
неотрицательны.
. Правда, в последнем
случае нам потребуется, чтобы все цены a[i][j] были
неотрицательны.
9.1.4.
Найти наименьшую стоимость проезда 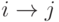 для всех i, j за время
для всех i, j за время  .
.
Решение. Для  через A(i,j,k)
обозначим наименьшую стоимость маршрута из i в j,
если в качестве пересадочных разрешено использовать только
пункты с номерами не больше k. Тогда
через A(i,j,k)
обозначим наименьшую стоимость маршрута из i в j,
если в качестве пересадочных разрешено использовать только
пункты с номерами не больше k. Тогда
A(i,j,0) = a[i][j],
A(i,j,k+1)=min(A(i,j,k), A(i,k+1,k)+{A(k+1,j,k))(два варианта соответствуют неиспользованию и использованию пункта k+1 в качестве пересадочного; отметим, что в нем незачем бывать более одного раза).
Этот алгоритм называют алгоритмом Флойда.
9.1.5.
Как проверить за  действий, имеет ли граф с n
вершинами
циклы с отрицательной суммой?
действий, имеет ли граф с n
вершинами
циклы с отрицательной суммой?
Указание.
Можно применять алгоритм Флойда, причем разрешать  в
в 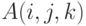 , пока не появится первый отрицательный цикл.
, пока не появится первый отрицательный цикл.
9.1.6.
Имеется  валют и таблица обменных курсов (сколько флоринов дают
за талер и т.п.). Коммерсант хочет неограниченно обогатиться, обменивая
свой начальный капитал туда-сюда по этим курсам. Как проверить,
возможно ли это?
валют и таблица обменных курсов (сколько флоринов дают
за талер и т.п.). Коммерсант хочет неограниченно обогатиться, обменивая
свой начальный капитал туда-сюда по этим курсам. Как проверить,
возможно ли это?
Указание. После логарифмирования деньги уподобляются расстояниям.
