| Россия, Пошатово |
Разные алгоритмы на графах
9.2. Связные компоненты, поиск в глубину и ширину
Наиболее простой случай задачи о кратчайших путях - если
все цены равны  или
или  . Другими словами, мы
интересуемся возможностью попасть из
. Другими словами, мы
интересуемся возможностью попасть из  в
в  , но за
ценой не постоим. В других терминах: мы имеем ориентированный
граф (картинку из точек, некоторые из которых соединены
стрелками) и нас интересуют вершины, доступные из
данной.
, но за
ценой не постоим. В других терминах: мы имеем ориентированный
граф (картинку из точек, некоторые из которых соединены
стрелками) и нас интересуют вершины, доступные из
данной.
Для этого случая задачи о кратчайших путях приведенные в предыдущем разделе алгоритмы - не наилучшие. В самом деле, более быстрая рекурсивная программа решения этой задачи приведена в "лекции 7" , а нерекурсивная - в "лекции 6" . Сейчас нас интересует такая задача: не просто перечислить все вершины, доступные из данной, но перечислить их в определенном порядке. Два популярных случая - поиск в ширину и в глубину.
Поиск в ширину.
Надо перечислить все вершины ориентированного графа,
доступные из данной, в порядке увеличения длины пути от
нее. (Тем самым мы решим задачу о кратчайших путях, когда
цены ребер равны  или
или  .)
.)
9.2.1.
Придумать алгоритм решения этой задачи с числом действий не
более 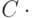 (число ребер, выходящих из интересующих нас
вершин).
(число ребер, выходящих из интересующих нас
вершин).
Решение. Эта задача рассматривалась в
"лекции 6"
, задача 6.3.9. Здесь мы приведем подробное решение.
Пусть num[i] - количество ребер, выходящих из i, ![{out[i][1]},\ldots,{out[i][num[i]]}](/sites/default/files/tex_cache/67097aec6d320d19f4a5a8e7529c0567.png) - вершины, куда
ведут ребра. Вот программа, приведенная ранее:
- вершины, куда
ведут ребра. Вот программа, приведенная ранее:
procedure Доступные (i: integer);
| {напечатать все вершины, доступные из i, включая i}
| var X: подмножество 1..n;
| P: подмножество 1..n;
| q, v, w: 1..n;
| k: integer;
begin
| ...сделать X, P пустыми;
| writeln (i);
| ...добавить i к X, P;
| {(1) P = множество напечатанных вершин; P содержит i;
| (2) напечатаны только доступные из i вершины;
| (3) X - подмножество P;
| (4) все напечатанные вершины, из которых выходит
| ребро в ненапечатанную вершину, принадлежат X}
| while X непусто do begin
| | ...взять какой-нибудь элемент X в v;
| | for k := 1 to num [v] do begin
| | | w := out [v][k];
| | | if w не принадлежит P then begin
| | | | writeln (w);
| | | | добавить w в P;
| | | | добавить w в X;
| | | end;
| | end;
| end;
end;Тогда нам было безразлично, какой именно элемент множества X выбирается. Если мы будем считать X очередью (первым пришел - первым ушел), то эта программа напечатает все вершины, доступные из i, в порядке возрастания их расстояния от i (числа ребер на кратчайшем пути из i ). Докажем это.
Обозначим через  множество всех вершин, расстояние
которых от i (в описанном смысле) равно
множество всех вершин, расстояние
которых от i (в описанном смысле) равно  . Имеет
место такое соотношение:
. Имеет
место такое соотношение:

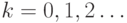 в ходе работы
программы будет такой момент (после очередной итерации
цикла while ), когда
в ходе работы
программы будет такой момент (после очередной итерации
цикла while ), когда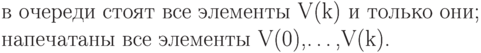
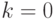 - это состояние перед циклом.) Рассуждая по
индукции, предположим, что в очереди скопились все элементы
- это состояние перед циклом.) Рассуждая по
индукции, предположим, что в очереди скопились все элементы  . Они будут просматриваться в цикле, пока не кончатся
(поскольку новые элементы добавляются в конец, они не
перемешаются со старыми). Концы ведущих из них ребер, если
они уже не напечатаны, печатаются и ставятся в очередь - то
есть все как в записанном выше соотношении для
. Они будут просматриваться в цикле, пока не кончатся
(поскольку новые элементы добавляются в конец, они не
перемешаются со старыми). Концы ведущих из них ребер, если
они уже не напечатаны, печатаются и ставятся в очередь - то
есть все как в записанном выше соотношении для  .
Так что когда все старые элементы кончатся, в очереди будут
стоять все элементы
.
Так что когда все старые элементы кончатся, в очереди будут
стоять все элементы  .
.