| Россия, Пошатово |
Анализ игр
11.1. Примеры игр
11.1.1.
Двое играют в такую игру: на столе лежит 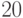 спичек; играющие
по очереди могут взять от
спичек; играющие
по очереди могут взять от  до
до  спичек; кто не может
сделать хода (спичек не осталось) - проигрывает. Кто
выигрывает при правильной игре?
спичек; кто не может
сделать хода (спичек не осталось) - проигрывает. Кто
выигрывает при правильной игре?
Решение. Второй выигрывает, если будет дополнять ход
первого до 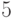 спичек (если первый берет одну, второй
должен взять четыре и так далее). Тогда после четырех
раундов спичек не останется и первый проиграет.
спичек (если первый берет одну, второй
должен взять четыре и так далее). Тогда после четырех
раундов спичек не останется и первый проиграет.
11.1.2.
Кто выиграет - первый или второй - если спичек не 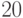 ,
а
,
а 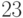 ?
?
Решение. Первый: если он возьмет три спички, то станет вторым в уже разобранной игре и потому сможет выиграть.
Аналогично получается ответ и для произвольного числа
спичек (  ): если
): если  кратно пяти, то выигрывает второй, а если нет, то
первый.
кратно пяти, то выигрывает второй, а если нет, то
первый.
11.1.3. Изменим условия игры: пусть взявший последнюю спичку проигрывает. Кто теперь выигрывает при правильной игре?
11.1.4.
Пусть теперь игрокам разрешено брать  ,
,  или
или  спички, а кто не может сделать ход, проигрывает. Кто
выигрывает при правильной игре, если вначале
было
спички, а кто не может сделать ход, проигрывает. Кто
выигрывает при правильной игре, если вначале
было 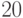 спичек?
спичек?
Решение. Здесь уже не так просто сразу указать выигрышную
стратегию для первого или второго. Начнем с небольшого
числа спичек, изобразив разрешенные ходы в виде стрелок (рис. 11.1.):
Игрок, оказавшийся в позиции  , проигрывает (таковы
правила), поэтому соответствующий кружок пометим буквой П.
Игрок, оказавшийся в позициях
, проигрывает (таковы
правила), поэтому соответствующий кружок пометим буквой П.
Игрок, оказавшийся в позициях  ,
,  или
или  , выигрывает,
поскольку он может забрать все спички и перевести
противника по стрелке в позицию
, выигрывает,
поскольку он может забрать все спички и перевести
противника по стрелке в позицию  . Поэтому мы пометим эти
позиции буквой В. Теперь ясно, что позиция
. Поэтому мы пометим эти
позиции буквой В. Теперь ясно, что позиция  является
проигрышной: из нее можно пойти только в
является
проигрышной: из нее можно пойти только в  и
и  ,
и тогда
противник (как мы уже знаем) выиграет. Пометим ее буквой П.
Далее замечаем, что позиции
,
и тогда
противник (как мы уже знаем) выиграет. Пометим ее буквой П.
Далее замечаем, что позиции  ,
, 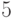 и
и 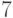 будут
выигрышными (поскольку из них можно попасть в проигрышную
для противника позицию
будут
выигрышными (поскольку из них можно попасть в проигрышную
для противника позицию  ; заметим, что из позиции
; заметим, что из позиции  можно выиграть и быстрее, пойдя в
можно выиграть и быстрее, пойдя в  ). Теперь видно, что
позиция
). Теперь видно, что
позиция 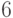 проигрышная (все стрелки из нее ведут
в выигрышные для противника позиции),
проигрышная (все стрелки из нее ведут
в выигрышные для противника позиции),  - выигрышная,
- выигрышная, 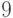 - проигрышная и так далее с периодом
- проигрышная и так далее с периодом  .
.
Таким образом, если число спичек делится на  , то позиция
проигрышная, если нет - то выигрышная. Поэтому в игре
с
, то позиция
проигрышная, если нет - то выигрышная. Поэтому в игре
с 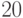 спичками первый игрок выигрывает.
спичками первый игрок выигрывает.
11.1.5. Как он для этого должен играть?
Решение. Ставить противника в проигрышную позицию, то есть
следить, чтобы после его хода число спичек было кратно трем
(в частности, в начале игры взять  спички, чтобы
осталось
спички, чтобы
осталось 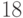 ).
).
11.1.6.
На столе лежат две кучки спичек: в одной  ,
в другой
,
в другой  .
За один ход разрешается взять любое (ненулевое) число
спичек, но только из одной кучки (можно взять все спички
в ней); кто не может сделать ход, проигрывает. Кто
выигрывает при правильной игре?
.
За один ход разрешается взять любое (ненулевое) число
спичек, но только из одной кучки (можно взять все спички
в ней); кто не может сделать ход, проигрывает. Кто
выигрывает при правильной игре?
Ответ: при  выигрывает второй, при
выигрывает второй, при 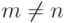 -
первый.
-
первый.
11.1.7. На шахматной доске стоит ладья, которую игроки по очереди двигают, при этом разрешено сдвигать ее влево и вниз (оставлять на месте нельзя); кто не может сделать ход, проигрывает. Кто выигрывает при правильной игре?
Указание. Как эта игра связана с предыдущей?
11.1.8.
Имеется  кучек из
кучек из 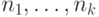 спичек; за один ход
можно взять любое (ненулевое) число спичек, но только из
одной кучи (можно взять все спички в ней); кто не может
сделать ход, проигрывает. Кто выигрывает при правильной
игре?
спичек; за один ход
можно взять любое (ненулевое) число спичек, но только из
одной кучи (можно взять все спички в ней); кто не может
сделать ход, проигрывает. Кто выигрывает при правильной
игре?
Решение. Запишем числа 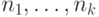 в двоичной системе
счисления друг под другом, как если бы мы собирались их
складывать. Если в каждом разряде при этом оказалось четное
число единиц, то выигрывает второй, в остальных случаях -
первый. В самом деле, если во всех разрядах четное число
единиц, то после уменьшения одного из чисел какой-то из
его разрядов изменится и в этом разряде получится нечетное
число единиц. (Это соответствует тому, что из проигрышной
позиции любой ход ведет в выигрышную.) Если же в некоторых
("плохих") разрядах нечетное число единиц, возьмем
старший плохой разряд и то из чисел, которое содержит
в этом разряде единицу. Тогда, изменив в этом числе все
плохие разряды, получим меньшее число, которое поставит
противника в проигрышную позицию. (См. правила для
выигрышных и проигрышных позиций в следующем разделе.)
в двоичной системе
счисления друг под другом, как если бы мы собирались их
складывать. Если в каждом разряде при этом оказалось четное
число единиц, то выигрывает второй, в остальных случаях -
первый. В самом деле, если во всех разрядах четное число
единиц, то после уменьшения одного из чисел какой-то из
его разрядов изменится и в этом разряде получится нечетное
число единиц. (Это соответствует тому, что из проигрышной
позиции любой ход ведет в выигрышную.) Если же в некоторых
("плохих") разрядах нечетное число единиц, возьмем
старший плохой разряд и то из чисел, которое содержит
в этом разряде единицу. Тогда, изменив в этом числе все
плохие разряды, получим меньшее число, которое поставит
противника в проигрышную позицию. (См. правила для
выигрышных и проигрышных позиций в следующем разделе.)
11.1.9.
В ряд лежат  ящиков, в каждом из них по монете. За один
ход игрок может взять любую монету или любые две монеты из
соседних ящиков; кто не может сделать ход, проигрывает. Кто
выигрывает при правильной игре?
ящиков, в каждом из них по монете. За один
ход игрок может взять любую монету или любые две монеты из
соседних ящиков; кто не может сделать ход, проигрывает. Кто
выигрывает при правильной игре?
Решение. Первый: он должен взять одну или две монеты в центре, а потом симметрично повторять ходы второго.

