Анализ игр

11.5. Ретроспективный анализ

Существенно ли описанное в прошлом разделе улучшение алгоритма (переход от полного перебора к -процедуре)? С одной стороны, да: в нашем примере переход от 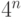к 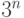дает выигрыш в 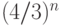раз, а 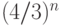экспоненциально растет с ростом . С другой стороны, экспонента остается экспонентой, даже если ее показатель уменьшается с до , поэтому надежды полностью проанализировать даже не очень сложную и долгую игру таким способом почти нет.

Поэтому на практике обычно выбирают некоторую оценку позиции - легко вычислимую функцию, которая по мнению практиков как-то отражает преимущество того или иного игрока (скажем, материальный перевес в шахматах). Затем вместо настоящей игры рассматривают ограниченную игру, в которой делается сравнительно небольшое число ходов, а затем результатом игры считается оценка полученной позиции, и в этой игре выполняют перебор (применяя -оптимизацию). Конечно, это ничего не гарантирует в настоящей игре, но что поделаешь.

Бывают, однако, и ситуации, когда удается определить цену данной позиции точно. Это удается сделать для шахматных эндшпилей с небольшим числом фигур - например, можно рассчитать, за какое минимальное число ходов можно поставить мат королем, слоном и конем против одинокого короля в заданных начальных условиях. Заметим, что при этом число ходов может измеряться десятками, а каждый ход имеет десятки вариантов, поэтому о полном переборе (или даже о несколько сокращенном) не может идти и речи.

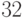11.5.1. Придумать другой подход, использующий ограниченность общего числа возможных позиций (скажем, для четырех упомянутых фигур на шахматной доске это "мегапозиций"; с учетом очередности хода будет мегапозиции; массив такого размера помещается в память современных компьютеров без труда).

Решение. Заведем массив, отведя ячейку для каждой позиции. Просмотрим его один раз и отметим все матовые позиции (записав туда число в знак того, что позиция выигрышная и до выигрыша осталось ходов). Затем просмотрим массив еще раз и пометим как проигрышные все позиции, из которых можно пойти лишь в матовые (напишем там в знак того, что можно протянуть лишь еще ход). Затем отметим все позиции, из которых есть ход в позиции с числом , написав там . Затем - позиции, из которых все ходы ведут в позиции или , написав там 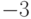, и т.п. Так будем делать до тех пор, пока будут появляться новые пометки. Как только это кончится, для каждой позиции будет известно, можно ли в ней выиграть и сколько ходов для этого нужно.

Фактически эта процедура повторяет доказательство теоремы Цермело (но дополнительно мы получаем информацию о том, сколько ходов до выигрыша или проигрыша при наилучшей игре).

11.5.2. Могут ли при этом остаться неотмеченные позиции и чему они соответствуют?

Ответ. Это позиции, в которых оба игрока могут гарантировать сколь угодно длинную игру без проигрыша. Впрочем, правило троекратного повторения позиции в шахматах в этом случае позволяет считать партию ничейной.

А.Л. Брудно заметил, что есть ситуация, в которой такой анализ требует совсем небольших ресурсов и может быть реализован на очень небольшой памяти, хотя для человека соответствующая задача не проста: пусть белые имеют короля на поле c3, которого им запрещено двигать, и ферзя (на каком-то другом поле) и хотят поставить мат одинокому черному королю. Ограничение (неподвижность короля), затрудняющее жизнь человеку-шахматисту, облегчает анализ (уменьшая количество позиций почти что в раза за счет того, что не надо рассматривать разные положения короля!)

Использование таблицы описанного типа можно считать применением метода динамического программирования (мы не вычисляем цену игры для одной и той же позиции снова и снова, обходя дерево, а заполняем таблицу цен систематически).