|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Наибольший общий делитель и последовательности полиномиальных остатков
Границы для коэффициентов делителя полинома
Вычисляя евклидову последовательность полиномиальных остатков,
мы видели, что коэффициенты промежуточных многочленов могут расти
достаточно быстро. При этом коэффициенты наибольшего общего
делителя, как правило, оказываются небольшими. В этом параграфе мы
постараемся найти оценки для коэффициентов многочленов, делящих
заданный многочлен с целыми коэффициентами. Первая гипотеза,
приходящая на ум, состоит в том, что если ![\smu{1}
f(x),g(x)\in \mathbb Z[x]](/sites/default/files/tex_cache/8d94490924df742590003db167ad841c.png) и
и 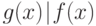 , то коэффициенты
делителя не превосходят по абсолютной величине коэффициентов
делимого. К сожалению,
, то коэффициенты
делителя не превосходят по абсолютной величине коэффициентов
делимого. К сожалению,
7.1. ПРИМЕР. Рассмотрим многочлены
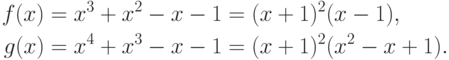
 .
.Этот пример легко обобщается, например, путем умножения обоих исходных
многочленов на  .
.
Неравенство Коши
Оценку для коэффициентов делителей полинома будем выводить из известного неравенства Коши, которое дает оценку абсолютной величины корня полинома.
ТЕОРЕМА.
Пусть  ,
,
 |
( 7.1) |
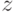 полинома
полинома  удовлетворяет неравенству
удовлетворяет неравенству |
( 7.2) |
ДОКАЗАТЕЛЬСТВО.
Пусть 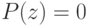 . Если
. Если  , то утверждение теоремы
тривиально.
Предположим, что
, то утверждение теоремы
тривиально.
Предположим, что  и положим
и положим  .
По предположению
.
По предположению


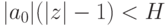 .
.Разумеется, эта оценка не является единственно возможной. Ниже приведены еще две оценки, первая из которых также принадлежит Коши, а вторая — Кнуту:

Каждая из этих оценок дает также границу и для минимального модуля
корня полинома (в предположении, что свободный член полинома
ненулевой) — заменяем в исходном полиноме  на
на  , другими
словами, ищем наибольший корень полинома
, другими
словами, ищем наибольший корень полинома 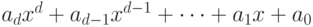 , обратный к
которому будет
наименьшим корнем исходного полинома.
, обратный к
которому будет
наименьшим корнем исходного полинома.
Воспользуемся неравенством Коши для получения оценки коэффициентов делителя полинома, которая известна как неравенство Ландау. Ландау
Неравенство Ландау
Пусть  . Положим
. Положим
 |
( 7.3) |
ТЕОРЕМА. Предположим, что полином  задан формулой
(7.1). Пусть
задан формулой
(7.1). Пусть  — корни полинома
— корни полинома  . Положим
. Положим

 .
.Для доказательства теоремы нам понадобится
ЛЕММА. Если 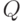 — полином и
— полином и 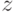 —
комплексное число, то
—
комплексное число, то
 |
( 7.4) |
ДОКАЗАТЕЛЬСТВО. Пусть  . Тогда квадрат
выражения в левой части равенства (7.4) равен
. Тогда квадрат
выражения в левой части равенства (7.4) равен

 ). Этому же выражению равен и
квадрат правой
части.
). Этому же выражению равен и
квадрат правой
части.ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ.
Пусть 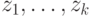 — корни полинома
— корни полинома  ,
лежащие вне единичного круга. Тогда
,
лежащие вне единичного круга. Тогда  . Положим
. Положим
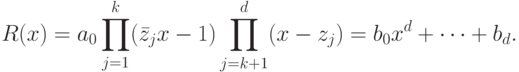
 . Однако
. Однако ![\smu{1} \|R\|^2\geq\|b_0\|^2
= [M(P)]^2](/sites/default/files/tex_cache/73fb14e70f3889ead8c715055337b6c9.png) .
.7.5. ТЕОРЕМА. Пусть  ,
,  — делитель полинома
— делитель полинома  , задаваемого
формулой (7.1). Тогда
, задаваемого
формулой (7.1). Тогда
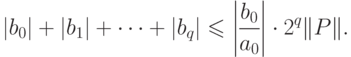
ДОКАЗАТЕЛЬСТВО. Легко проверяется, что
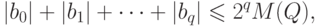
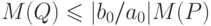 , и из неравенства Ландау
следует, что
, и из неравенства Ландау
следует, что  .
.7.6. УПРАЖНЕНИЕ. Пусть ![f(x) \in \Z[x]](/sites/default/files/tex_cache/868767280ebd38aef2c4f1cc2c71e1b5.png) и
и 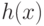 — делитель полинома
— делитель полинома  .
Предположим, что
.
Предположим, что  . Тогда
. Тогда

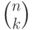 используется здесь и неоднократно в
дальнейшем
для обозначения биномиальных коэффициентов, т. е. числа сочетаний из
используется здесь и неоднократно в
дальнейшем
для обозначения биномиальных коэффициентов, т. е. числа сочетаний из  по
по  .)
.)Другие полезные границы можно найти, например, в работе [ 25 ] .

