Наибольший общий делитель и последовательности полиномиальных остатков

Модулярный алгоритм вычисления НОД многочленов.

Пусть p — простое число. Любое целое число m можно рассматривать как представитель соответствующего класса вычетов по модулю p, т. е. числу m можно однозначно поставить в соответствие некоторый элемент из поля . В частности, любому многочлену можно однозначно поставить в соответствие многочлен .

Вернемся к примеру 6.7. Многочлены

можно рассматривать как элементы кольца для любого простого p. Можно вычислить их наибольший общий делитель в . При этом у нас не возникнет проблем с ростом коэффициентов, поскольку мы можем пользоваться системой представителей из множества {0, 1, . . . .p - 1}. Полагая p = 5, мы без особого труда убеждаемся, что многочлены a(x) и b(x) взаимно просты в кольце . Можно ли из этого сделать вывод, что многочлены a(x) и b(x) взаимно просты в кольце ? Оказывается, можно. Доказательство этого факта основано на следующих утверждениях.

6.8. ПРЕДЛОЖЕНИЕ. Описанное выше отображение , такое, что 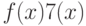является гомоморфизмом колец, т. е. сумма переходит в сумму, а произведение—в произведение. В частности, если g(x) | f(x) в , то g_p(x) | f_p(x) в .

6.9. ПРЕДЛОЖЕНИЕ. Предположим, что —примитивные многочлены и простое число p не делит старшие коэффициенты многочленов a(x) и b(x). Если НОД(a_p(x), b_p(x)) = 1 в , то НОД(a(x), b(x)) = 1 в .

6.10. УПРАЖНЕНИЕ. Показать, что оба условия в предложении 6.9 являются существенными, т. е. если многочлены не являются примитивными или p делит их старшие коэффициенты, то из НОД(a_p(x), b_p(x)) = 1 в не следует, что НОД(a(x), b(x)) = 1 в .

6.11. ПРЕДЛОЖЕНИЕ. Предположим, что — примитивные многочлены, такие, что НОД(a(x), b(x))=1 в . Тогда НОД(a_p(x), b_p(x))=1 в для почти всех простых чисел p.

ДОКАЗАТЕЛЬСТВО. Без потери общности мы можем считать, что рассматриваются только простые числа, которые не делят ни старший коэффициент многочлена a(x), ни старший коэффициент многочлена b(x). Условие НОД(a_p(x), b_p(x)) = 1 означает, что результант Resp(a_p, b_p) этих многочленов, рассматриваемых как элементы кольца , не обращается в нуль. Чтобы вычислить Resp(a_p, b_p), нам достаточно вычислить результант Res(a, b) многочленов a(x), b(x) в кольце и взять образ этого результанта по модулю p. Результант Res(a, b) является ненулевым целым числом (так как исходные многочлены по условию взаимно просты) и делится только на конечное число простых чисел.

6.12. ОПРЕДЕЛЕНИЕ. Пусть —примитивные многочлены, такие, что НОД(a(x), b(x))=1 в . Простое число p назовем плохой редукцией, если либо p делит старший коэффициент хотя бы одного из многочленов a(x), b(x), либо .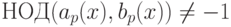

6.13. ЗАДАЧА. Для примитивных многочленов найти ограничение сверху для числа плохих редукций (или ограничение сверху для их произведения).

Для решения этой задачи могут пригодиться результаты, приведенные в "Алгоритмы Кронекера. Разложение на множители, свободные от квадратов. Факторизация" .

Итак, мы можем сформулировать следующий алгоритм проверки взаимной простоты примитивных многочленов .

А 7. АЛГОРИТМ (Проверки взаимной простоты многочленов).

В действительности, модулярный метод может быть применен не только для проверки взаимной простоты многочленов, но и для нахождения их НОД.

Следующее предложение обобщает предложение 6.11.

6.14. ПРЕДЛОЖЕНИЕ. Предположим, что —примитивные многочлены и d(x) = НОД(a(x), b(x)) в . Предположим, что p — простое число, которое не делит ни старший коэффициент многочлена a(x), ни старший коэффициент многочлена b(x ). Пусть в . Тогда deg и для почти всех p.

ДОКАЗАТЕЛЬСТВО. Из предложения 6.8 следует, что d_p(x) является общим делителем многочленов a_p(x) и b_p(x)) в , т. е. . Следовательно, . Применяя предложение 6.11 к многочленам a(x)/d(x ) и b(x)/d(x), получим, что для почти всех p.

Обобщим определение 6.12 следующим образом.

6.15. ОПРЕДЕЛЕНИЕ. Пусть —примитивные многочлены. Простое число p назовем плохой редукцией, если либо p делит старший коэффициент хотя бы одного из многочленов a(x), b(x), либо .

Можно ли утверждать, что ? Для ответа на этот вопрос вспомним, что НОД определен с точностью до умножения на обратимые элементы кольца, т. е. , следовательно, и определены с точностью до умножения на , а 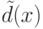определен с точностью до умножения на ненулевые элементы поля . Таким образом, среди возможных значений 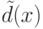будут , но, в общем случае, ими значения 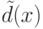не исчерпываются.

Наша ближайшая цель — разработать алгоритм вычисления наибольшего общего делителя примитивных многочленов с целочисленными коэффициентами, основываясь на следующих соображениях. Выбираем несколько простых чисел , которые должны быть достаточно маленькими (чтобы вычисления в полях вычетов выполнялись без применения длинной арифметики). Вычисляем наибольшие общие делители многочленов с коэффициентами из полей вычетов по модулю . Отбрасываем плохие редукции. Применяя китайскую теорему об остатках к коэффициентам многочленов, находим требуемый НОД.