Наибольший общий делитель и последовательности полиномиальных остатков

Алгоритмы вычисления НОД(a,b) в кольцах иногочленов k[x] и Z[x]

Сформулируем алгоритмы, предложенные ранее в качестве упражнения. Во всех предложенных ниже алгоритмах считаем, что a и b — натуральные числа, следовательно, ненулевые.

А1. АЛГОРИТМ (НОД1).

Данный алгоритм использует операции сравнения натуральных чисел, вычитания натуральных чисел и присваивания переменной значения натурального числа. Оценивая сложность предложенного алгоритма, можно рассматривать эти операции как элементарные. В теле цикла "пока" выполняется две операции сравнения, одна операция вычитания и одна операция присваивания. Цикл выполняется не более max(a, b) раз. Таким образом, сложность алгоритма равна O(max(a, b)).

Однако, более естественно рассматривать в качестве элементарных битовые операции.

5.22. УПРАЖНЕНИЕ. Показать, что если max(a, b) = n, то сложность вычисления НОД(a, b) по предложенному алгоритму равна O(n log₂ n) битовых операций.

А2. АЛГОРИТМ (Евклида).

В алгоритме Евклида использовано стандартное обозначение x (mod y) для остатка от деления x на y. Легко показать, что после двух делений делимое уменьшается, как минимум, в два раза. Значит, количество повторений цикла равно O(log₂ n), где n=max(a, b). Определяя битовую сложность алгоритма Евклида, мы должны учитывать, что сложность операции деления зависит от количества цифр квадратично. Таким образом, мы получаем оценку для битовой сложности алгоритма Евклида. Более тщательный анализ позволяет доказать оценку .

Можно показать, что, в определенном смысле, наихудший вариант для алгоритма Евклида представляют последовательные числа Фиббоначчи.

5.23. УПРАЖНЕНИЕ. Показать, что если a = F_n+1, b = F_n — со- ответствующие числа Фиббоначчи, то остатки в алгоритме Евклида принимают последовательно значения F_n-1, . . . , F₂ = 1.

5.24. УПРАЖНЕНИЕ. Показать, что если a > b и — последовательные остатки, получаемые в алгоритме Евклида, то a > F_n+1, где F_k — k -ое число Фиббоначчи.

Легко видеть, что алгоритм Евклида применим в любом евкли- довом кольце, т. е. условия 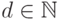и 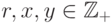можно заменить на , где R — любое евклидово кольцо.

5.25. УПРАЖНЕНИЕ. Что произойдет, если в алгоритме Евклида a и b — отрицательные или нулевые целые числа?

Следующий алгоритм использует специфику машинной арифметики, основанной на системе счисления по основанию 2, в которой операции умножения и деления на 2 сводятся к сдвигу, следовательно, выполняются очень быстро.

А3. АЛГОРИТМ (бинарный НОД).

5.26. ЗАМЕЧАНИЕ. В конструкции выбор выполняются только действия для первого истинного условия в операторах при. Таким образом, на первые два условия мы можем попасть, когда один из аргументов четный, а другой — нечетный. На последние два условия можно попасть, только когда оба аргумента нечетны. Учитывая, что при вычитании нечетного числа из нечетного получается четное, можно результат сразу разделить на 2, т. е. строки

при x > y делать x := x - y
		при x < y делать y := y - x

заменить строками

при x > y делать x := (x - y)/2
		при x < y делать y := (y - x)/2

Очевидно, что при каждом повторении тела цикла последнего алгоритма хотя бы один аргумент уменьшается в два раза. Значит, количество повторений цикла равно O(log2 n), где n = max(a, b). Определяя битовую сложность бинарного алгоритма, мы должны учитывать, что сложность операций, выполняемых в теле цикла, зависит от количества цифр линейно, т. е. битовая сложность бинарного алгоритма равна .

Приведем еще алгоритм вычисления НОД, основанный на свойстве факториальности кольца .

А4. АЛГОРИТМ ( НОД через примарное разложение).