|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Наибольший общий делитель и последовательности полиномиальных остатков
Что касается необходимого количества редукций (количества простых чисел, по модулю которых выполняются вычисления), то можно поступить одним из следующих способов:
- оценить заранее достаточное число редукций, пользуясь, например, оценками для коэффициентов делителей заданного многочлена, приведенными в "Алгоритмы Кронекера. Разложение на множители, свободные от квадратов. Факторизация" ;
- после каждой редукции пересчитывать коэффициенты искомого НОД, пользуясь КТО; если применение новой редукции не меняет этих коэффициентов, то проверить, делит ли полученный многочлен исходные. Если да, то задача решена, иначе выполнять следующие редукции.
Отметим, что в этой задаче, применяя КТО, мы должны находить числа
с данными вычетами не из множества неотрицательных чисел 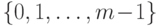 , а из симметричной системы
, а из симметричной системы 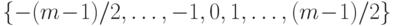 (при
четном
(при
четном  , т. е. когда в качестве одного из модулей используется 2,
система получается немного несимметричной: от
, т. е. когда в качестве одного из модулей используется 2,
система получается немного несимметричной: от 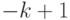 до
до  , где
, где 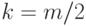 ).
).
Основная же проблема состоит в том, как согласовать вычисления
для различных значений  . Здесь можно предложить два
подхода.
. Здесь можно предложить два
подхода.
Во-первых, можно свести задачу к случаю, когда искомый НОД
является нормированным многочленом. Для этого заметим, что старший
коэффициент искомого НОД делит старшие коэффициенты исходных
многочленов, а значит, делит НОД старших коэффициентов этих
многочленов. Обозначим этот НОД через  . Перейдем от переменной
. Перейдем от переменной  к переменной
к переменной 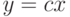 . Для этого нам понадобится
домножить
исходные многочлены на некоторые степени числа
. Для этого нам понадобится
домножить
исходные многочлены на некоторые степени числа  , чтобы после
замены
, чтобы после
замены 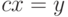 получить многочлены
получить многочлены 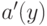 и
и 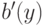 с
целочисленными коэффициентами. После этого решаем задачу для
многочленов
с
целочисленными коэффициентами. После этого решаем задачу для
многочленов 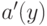 и
и 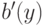 , выполняя все вычисления в
кольцах
вычетов над нормированными многочленами. Получаем
, выполняя все вычисления в
кольцах
вычетов над нормированными многочленами. Получаем  в
в ![\Z[y]](/sites/default/files/tex_cache/a3e10d5c62da41e372bbdb55d06ec7f7.png) . К сожалению,
. К сожалению, 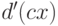 , в
общем случае, не является искомым наибольшим общим делителем, а
отличается от него некоторым целочисленным множителем. Чтобы найти
искомый НОД, достаточно вычислить примитивную часть многочлена
, в
общем случае, не является искомым наибольшим общим делителем, а
отличается от него некоторым целочисленным множителем. Чтобы найти
искомый НОД, достаточно вычислить примитивную часть многочлена 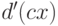 .
.
Недостаток этого метода в том, что при достаточно высоких степенях исходных
многочленов коэффициенты промежуточных многочленов (от  )
становятся
очень большими, что требует большего количества чисел
)
становятся
очень большими, что требует большего количества чисел  ,
используемых для редукций, и более громоздких вычислений при применении КТО.
,
используемых для редукций, и более громоздких вычислений при применении КТО.
А 8. АЛГОРИТМ (Модулярный НОД).
![\begin{align*}
&\text{Дано: \quad $a(x), b(x) \in Z[x]$}\\
&\text{Надо: \quad $d(x) = НОД(a(x), b(x))$}\\
&\text{начало}\\
&\text{$c := НОД(lc(a(x)), lc(b(x)))$}\\
&\text{выбрать нечетное простое $p$}\\
&\text{$m := p$}\\
&\text{$dm(x) := c * НОД(a_p(x), b_p(x))$ (в симметричной системе вычетов}\\
&\text{\quad \quad \quad по модулю $m$);}\\
&\text{цикл пока $p.p.(d_m(x))$ не делит $a(x) и b(x) в Z[x]$}\\
&\text{\quad выбрать следующее простое $p$}\\
&\text{\quad $d_p(x) := НОД(a_p(x), b_p(x))$}\\
&\text{\quad если $deg d_p(x) < deg d_m(x)$ то}\\
&\text{\quad \quad $m := p$}\\
&\text{\quad \quad $d_m(x) := c * d_p(x)$ (в симметричной системе вычетов}\\
&\text{\quad \quad \quad по модулю $m$);}\\
&\text{\quad иначе если $deg d_p(x) = deg d_m(x)$ то}\\
&\text{\quad \quad Применить КТО к $(m, p, d_m(x), c * d_p(x))$}\\
&\text{\quad конец если}\\
&\text{конец цикла}\\
&\text{вернуть$(d_m(x)$)}
\end{align*}](/sites/default/files/tex_cache/20536c4b876760598f290fecfc7e4034.png)
Предписание "Применить КТО к 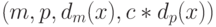 " означает
следующее. На входе:
" означает
следующее. На входе:  — простое число,
— простое число,  — натуральное
число, не делящееся на
— натуральное
число, не делящееся на  , коэффициенты многочленов
, коэффициенты многочленов 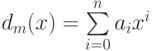 и
и ![c*d_p(x)=\smash[t]{\sum\limits_{i=0}^n}b_ix^i](/sites/default/files/tex_cache/f551867fc4f2bfce830ac3fcb48c9f12.png) рассматриваются как
представители смежных классов по модулю
рассматриваются как
представители смежных классов по модулю  и
и  соответственно.
Вычисляются числа
соответственно.
Вычисляются числа 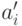 , такие что
, такие что 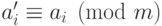 и
и 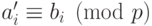 ,
, 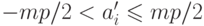 ,
, 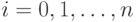 . На
выходе
. На
выходе 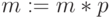 и
и 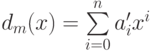 .
.
6.16. ЗАДАЧА. Доказать корректность представленного алгоритма.
6.17. ПРИМЕР.
Пользуясь модулярным алгоритмом, вычислим НОД многочленов  и
и  .
.
Наибольший общий делитель старших коэффициентов равен 4. Вычисляя  , получим
, получим  . Домножая
. Домножая  на 4 и переходя к симметричной системе вычетов, снова получим
на 4 и переходя к симметричной системе вычетов, снова получим 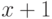 . Легко проверить, что полученный многочлен не делит ни один
из исходных многочленов.
. Легко проверить, что полученный многочлен не делит ни один
из исходных многочленов.
В качестве следующего простого числа берем  . Вычисляя
. Вычисляя  , получим
, получим 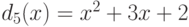 .
Поскольку
.
Поскольку 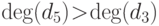 , заключаем, что
, заключаем, что  является "плохой
редукцией".
является "плохой
редукцией".
Переходим к  . Получаем
. Получаем 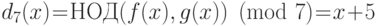 .
Домножая на 4, получим
.
Домножая на 4, получим 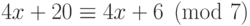 . Пользуясь
китайской теоремой об остатках, решаем систему сравнений
. Пользуясь
китайской теоремой об остатках, решаем систему сравнений
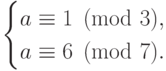
 . Переходя к симметричной системе
вычетов, получаем
. Переходя к симметричной системе
вычетов, получаем  . Убеждаемся, что
. Убеждаемся, что 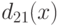 не
делит исходные многочлены в
не
делит исходные многочлены в ![\mathbb Q[x]](/sites/default/files/tex_cache/f3d1f8b27dd29107881f26927fbcc385.png) .
.Берем 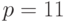 . Получаем
. Получаем 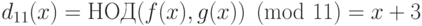 .
Домножая на 4, получим
.
Домножая на 4, получим 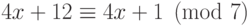 . Пользуясь
китайской теоремой об остатках, решаем систему сравнений
. Пользуясь
китайской теоремой об остатках, решаем систему сравнений
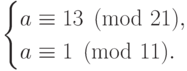
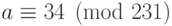 . Переход к симметричной системе вычетов
ничего не меняет, и в итоге мы получаем
. Переход к симметричной системе вычетов
ничего не меняет, и в итоге мы получаем 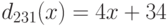 .
Убеждаемся, что
.
Убеждаемся, что 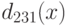 делит исходные многочлены в
делит исходные многочлены в ![\mathbb \Q[x]](/sites/default/files/tex_cache/1f5c10c2d211606dc871b1be697cf4aa.png) и
и 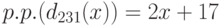 является наибольшим общим делителем
исходных многочленов.
является наибольшим общим делителем
исходных многочленов.
