|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Наибольший общий делитель и последовательности полиномиальных остатков
Пользуясь леммой Гаусса 6.2, мы можем разбить вычисление НОД(f(x), g(x)) в кольце ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) на следующие этапы:
на следующие этапы:
- найти наибольший общий делитель
 коэффициентов
многочленов f(x) и g(x) ;
коэффициентов
многочленов f(x) и g(x) ; - найти dq(x) = НОД(f(x), g(x)) в кольце
![\mathbb Q[x]](/sites/default/files/tex_cache/f3d1f8b27dd29107881f26927fbcc385.png) , нормированный таким образом, что
, нормированный таким образом, что ![dq(x)\in \mathbb Z[x]](/sites/default/files/tex_cache/e185c95742f4ccf47830466eeb234c2a.png) и коэффициенты многочлена dq(x) взаимно просты;
и коэффициенты многочлена dq(x) взаимно просты; -
НОД(f(x), g(x)) = dc · dq(x) в кольце
![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) .
.
Введем следующие определения.
6.3. ОПРЕДЕЛЕНИЕ. Наибольший общий делитель коэффициен-
тов многочлена ![f(x) \in \mathbb Z[x]](/sites/default/files/tex_cache/ef99ff92f5df8a33bd2d8ca08ea8be1a.png) называется содержанием этого многочлена и обозначается cont(f). Многочлен f(x)/ cont(f) называется примитивной частью многочлена f(x) и обозначается p. p.(f(x)).
называется содержанием этого многочлена и обозначается cont(f). Многочлен f(x)/ cont(f) называется примитивной частью многочлена f(x) и обозначается p. p.(f(x)).
Обратимся теперь к задаче нахождения наибольшего общего делителя двух полиномов p1(x), p2(x) в кольце ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) , при условии, что
все арифметические операции над коэффициентами выполняются не
в поле
, при условии, что
все арифметические операции над коэффициентами выполняются не
в поле  , а в кольце
, а в кольце  , являющимся не полем, а только областью
с однозначным разложением на множители. Из приведенных выше
рассуждений ясно, что мы можем вывести следующие важные соотношения:
, являющимся не полем, а только областью
с однозначным разложением на множители. Из приведенных выше
рассуждений ясно, что мы можем вывести следующие важные соотношения:
cont{НОД[p1(x), p2(x)]} = НОД{cont[p1(x)], cont[p2(x)]},
p. p.{НОД[p1(x), p2(x)]} = НОД{p. p.[p1(x)], p. p.[p2(x)]}.Поэтому задача нахождения наибольшего общего делителя произвольных полиномов сводится к задаче нахождения наибольшего общего делителя примитивных полиномов.
Рассмотрим два примитивных ненулевых полинома p1(x) и p2(x)
в ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) , у которых deg[p1(x)] = m и deg[p2(x)] = n, m > n. Поскольку
алгоритм деления полиномов с остатком требует точной делимости
старшего коэффициента делимого на старший коэффициент делителя, обычно этот процесс невозможно выполнить для полиномов p1(x) и p2(x) над целыми числами, не ослабляя требования делимости. Поэтому мы вводим процесс псевдоделения, который всегда
дает нам псевдочастное и псевдоостаток (prem), коэффициенты
которых являются целыми числами.
, у которых deg[p1(x)] = m и deg[p2(x)] = n, m > n. Поскольку
алгоритм деления полиномов с остатком требует точной делимости
старшего коэффициента делимого на старший коэффициент делителя, обычно этот процесс невозможно выполнить для полиномов p1(x) и p2(x) над целыми числами, не ослабляя требования делимости. Поэтому мы вводим процесс псевдоделения, который всегда
дает нам псевдочастное и псевдоостаток (prem), коэффициенты
которых являются целыми числами.
Псевдоделение означает предварительное умножение полинома p1(x) на {lc[p2(x)]}m-n+1, а затем применение алгоритма деления многочленов, когда известно, что все частные существуют, т. е.
![\{lc[p_2(x)]\}^{m-n+1}p_1(x)=p_2(x)q(x)+r(x),\quad \deg[r(x)]<\deg[p_2(x)],](/sites/default/files/tex_cache/12ea61e5c07c1adec18facf826665206.png)
где q(x) и r(x) — псевдочастное и псевдоостаток соответственно.
6.4. ПРИМЕР. Пользуясь псевдоделением в ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) , разделим p1(x) == x4 - 7x + 7 на p2(x) = 3x2 - 7. Для того, чтобы вычислить q(x)
и r(x), предварительно умножим p1(x) на 34-2+1 = 27, а затем,
применяя алгоритм деления многочленов, получаем q(x) = 9x2 + 21
и r(x) = -189x + 336. Читатель может убедиться, что алгоритм
деления многочленов не будет работать, если мы предварительно
домножим p1(x ) только на 3.
, разделим p1(x) == x4 - 7x + 7 на p2(x) = 3x2 - 7. Для того, чтобы вычислить q(x)
и r(x), предварительно умножим p1(x) на 34-2+1 = 27, а затем,
применяя алгоритм деления многочленов, получаем q(x) = 9x2 + 21
и r(x) = -189x + 336. Читатель может убедиться, что алгоритм
деления многочленов не будет работать, если мы предварительно
домножим p1(x ) только на 3.
Поэтому, пытаясь вычислить наибольший общий делитель полиномов p1(x) и p2(x), мы должны убедиться, что выполнимы все деления полиномов, встречающиеся в этом процессе, т. е. мы должны, используя псевдоделения, сформировать последовательность полиномиальных остатков. Таким образом, мы приходим к следующему обобщенному алгоритму Евклида для полиномов.
А 6. АЛГОРИТМ (GEA-P). Обобщенный алгоритм Евклида для многочленов над целыми числами G eneralized E uclidean A lgorithm for P olynomials over the Integers.
![\begin{align*}
&\text{Дано:\quad $p_1(x), p_2(x)$ - ненулевые полиномы в $ \mathbb Z[x]$;}\\
&\text{\quad \quad \quad$\deg[p_1(x)]=n_1$, $\deg[p_2(x)] = n_2$,$n_1\ge n_2$.}\\
&\text{Надо:\quad $НОД[p_1(x), p_2(x)]$, НОД многочленов $p_1(x)$ и $p_2(x)$.}\\
&\text{начало}\\
&\text{ \quad\quad\quad 1 [Вычисление НОД содержаний]}\\
&\text{\quad\quad\quad\quad $c:=НОД\{\cont[p_1(x)],\cont[p_2(x)]\}$.(Здесь мы используем }\\
&\text{\quad\quad\quad алгоритм Евклида для вычисления наибольшего общего де-}\\
&\text{\quad\quad\quad лителя двух целых чисел.)}\\
&\text{ \quad\quad 2 [Вычисление примитивных частей]}\\
&\text{\quad\quad\quad $p'_1(x):=p_1(x)/\cont[p_1(x)]; p'_2(x):=p_2(x)/\cont[p_2(x)]$.}\\
&\text{ \quad\quad3 [Построение PRS]}\\
&\text{\quad\quad\quad Вычислить $p'_1(x),p'_2(x),p_3(x),\dots,p_h(x)$.}\\
&\text{\quad\quad 4 [Выход]}\\
&\text{ \quad\quad\quad Если $\deg[p_h(x)] = 0$, то вернуть $НОД[p_1(x), p_2(x)]:=c$,}\\
&\text{ \quad\quad\quad иначе вернуть $НОД[p_1(x), p_2(x)]:=c\cdot \pp[p_h(x)]$.}\\
\end{align*}](/sites/default/files/tex_cache/10eb8527349a306b64ee18a90c7c7fbc.png)
Ясно, что время работы этого алгоритма зависит от того, насколько эффективно мы можем вычислять последовательность полиномиальных остатков  . Заметим, что
если
. Заметим, что
если ![n_i=\deg[p_i(x)]](/sites/default/files/tex_cache/da83bc8bcb03416c3db7d8a43f2b840d.png) , то в общем случае мы можем утверждать, что
члены этой последовательности удовлетворяют соотношениям
, то в общем случае мы можем утверждать, что
члены этой последовательности удовлетворяют соотношениям
![\{lc[p_{i+1}(x)]\}^{n_i-n_{i+1}+1}p_i(x)=p_{i+1}(x)q_i(x)+\beta_ip_{i+2}(x),\\
\deg[p_{i+2}(x)] < \deg[p_{i+1}(x)],
\end{gathered}\label{beta}](/sites/default/files/tex_cache/e334d8961ce9e3c9d40c75d65cffbf21.png)
где i = 1, 2, . . . , h - 1 для некоторого h. [Разумеется,  , i = 1, 2,где
, i = 1, 2,где 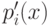 ,
, 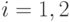 определены на шаге 2 алгоритма GEA-P ].
Если дан метод выбора коэффициентов
определены на шаге 2 алгоритма GEA-P ].
Если дан метод выбора коэффициентов 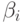 , то выписанное соотношение дает алгоритм построения PRS; очевидно, что условие завершения этого семейства алгоритмов — равенство нулю псевдоостатка.
, то выписанное соотношение дает алгоритм построения PRS; очевидно, что условие завершения этого семейства алгоритмов — равенство нулю псевдоостатка.
Ниже мы рассматриваем различные алгоритмы, полученные для
разных значений 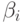 .
.
Евклидов алгоритм PRS.
Здесь 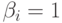 для всех
для всех  ,
т.е. каждый псевдоостаток
используется в том виде, в котором он получен. Это один из худших методов
построения PRS, приводящий к экспоненциальному росту коэффициентов.
,
т.е. каждый псевдоостаток
используется в том виде, в котором он получен. Это один из худших методов
построения PRS, приводящий к экспоненциальному росту коэффициентов.
6.5. ПРИМЕР. Рассмотрим полиномы  ,
, 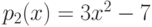 в
в ![\mathbb Z[x].](/sites/default/files/tex_cache/bc170df725727f37d5e10ddb329461c6.png) Очевидно, что
Очевидно, что ![\cont[p_1(x)]=\cont[p_2(x)]=1](/sites/default/files/tex_cache/60ce38bf9a98760dc95e95341c6c49dc.png) и
и  ,
, 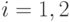 .
Мы имеем такую последовательность:
.
Мы имеем такую последовательность:

полученную при выполнении следующих псевдоделений:

Из шага 4 алгоритма GEA-P следует, что НОД[p1(x), p2(x)]=1. Отметим также, что в последнем псевдоделении коэффициенты имеют 8 десятичных цифр, поскольку (-441)2p3(x)=-8168202x+12252303.
Последовательность полиномиальных остатков этого примера называется полной, потому что степень каждого ее члена на единицу меньше степени предыдущего; два первых члена могут, конечно, иметь одинаковые степени. В противном случае последовательность называется неполной. Заметим, что не существует способа сказать a priori, будет ли PRS полной или неполной.
Экспоненциальный рост коэффициентов членов PRS в приведенном примере обусловлен тем, что полиномы этой последовательности не являются примитивными, т. е. то, что мы не избавляемся от их содержания, дает вредный эффект. Эта ситуация исправляется ниже.
