|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Целозначные многочлены и размерностные многочлены матриц и подмножеств в Nm
Определение целозначных многочленов и их основные свойства
11.1. ОПРЕДЕЛЕНИЕ.
Многочлен  от переменной
от переменной  с рациональными
коэффициентами называется целозначным
если
с рациональными
коэффициентами называется целозначным
если 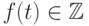 для всех достаточно больших
для всех достаточно больших 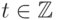 .
.
Очевидно, что всякий многочлен с целыми коэффициентами является целозначным. В качестве примера целозначного многочлена, коэффициенты которого не являются целыми числами, рассмотрим многочлен
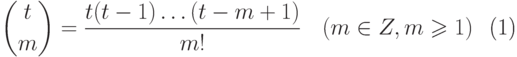 |
( 11.1) |
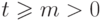 задает число сочетаний из
задает число сочетаний из  по
по  .
.Иногда мы будем рассматривать выражение  для
неположительных значений
для
неположительных значений  , полагая
, полагая
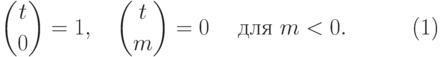 |
( 11.2) |
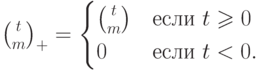
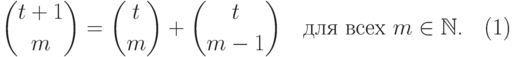 |
( 11.3) |
Следующее предложение дает некоторые соотношения между "биномиальными" целозначными многочленами, которые будут использоваться в дальнейшем.
11.2. ПРЕДЛОЖЕНИЕ.
Следующие соотношения выполняются для всех 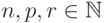 :
:
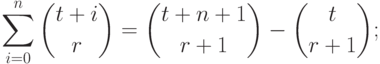 |
( 11.4) |
 |
( 11.5) |
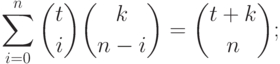 |
( 11.6) |
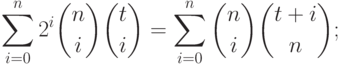 |
( 11.7) |
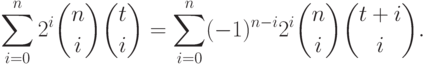 |
( 11.8) |
ДОКАЗАТЕЛЬСТВО.
Справедливость равенств (11.4) и (11.5) может быть легко
выведена из (11.3) индукцией по  .
.
Прежде чем доказывать (11.6)-(11.8), заметим, что если
значения целозначных многочленов  и
и 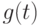 совпадают
для всех достаточно больших целых значений
совпадают
для всех достаточно больших целых значений  , то
, то  . Поэтому при доказательстве (11.6)-(11.8) мы
можем (и будем) предполагать, что
. Поэтому при доказательстве (11.6)-(11.8) мы
можем (и будем) предполагать, что 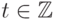 ,
,  .
.
Сравнивая коэффициенты при 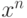 в тождестве
в тождестве 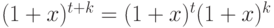 , мы получим (11.6). Для
того, чтобы получить
(11.7), сначала докажем, что
, мы получим (11.6). Для
того, чтобы получить
(11.7), сначала докажем, что
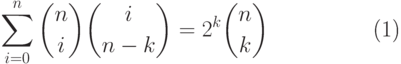 |
( 11.9) |
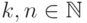 (как обычно, мы полагаем
(как обычно, мы полагаем  для
для 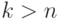 ).
Действительно, используя непосредственно проверяемое тождество
).
Действительно, используя непосредственно проверяемое тождество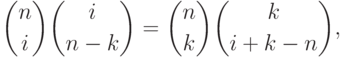
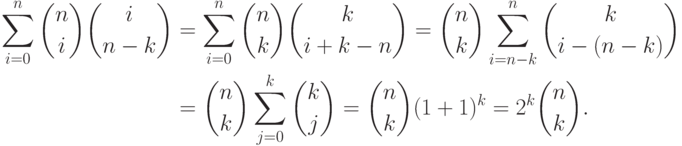
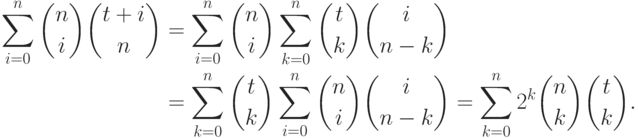
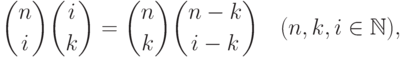
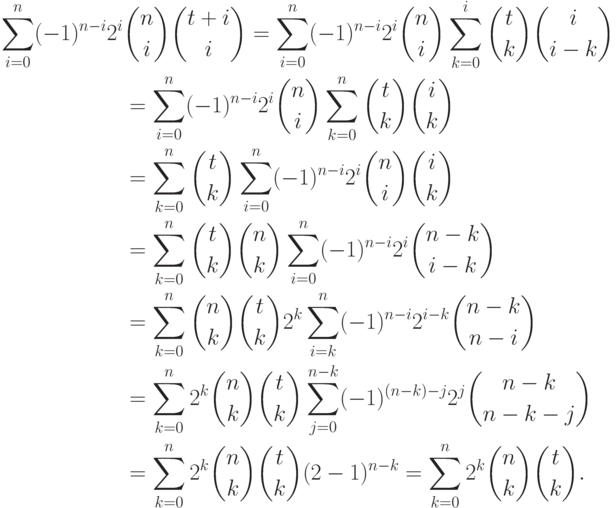
Заметим, что если  - целозначный многочлен, то его
первая разность
- целозначный многочлен, то его
первая разность 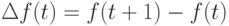 и следующие разности
и следующие разности  ,
, 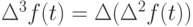 , \etc
также являются целозначными многочленами. В частности, из (11.3)
следует, что
, \etc
также являются целозначными многочленами. В частности, из (11.3)
следует, что
 |
( 11.10) |
11.3. ПРЕДЛОЖЕНИЕ. Пусть  - целозначный многочлен степени
- целозначный многочлен степени  . Тогда
. Тогда  можно представить в виде
можно представить в виде
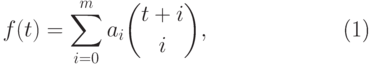 |
( 11.11) |
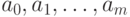 - целые числа, однозначно
определенные многочленом
- целые числа, однозначно
определенные многочленом  .
.ДОКАЗАТЕЛЬСТВО.
Разделив многочлен  на
на  в кольце
в кольце ![\mathbb Q[t]](/sites/default/files/tex_cache/4f86571a2c9dd7d0ff2b29aa9864c2e3.png) , мы получим
, мы получим 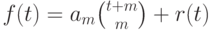 , где
, где 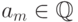 и
и 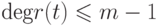 .
Разделив
.
Разделив 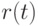 на
на 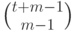 (в
(в ![\mathbb Q[t]](/sites/default/files/tex_cache/4f86571a2c9dd7d0ff2b29aa9864c2e3.png) ), мы получим
), мы получим  ,
где
,
где  . Продолжая этот процесс, мы придем к выражению
. Продолжая этот процесс, мы придем к выражению
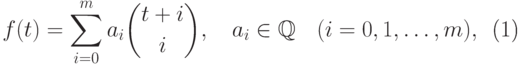 |
( 11.12) |
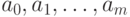 однозначно определены
многочленом
однозначно определены
многочленом  . Нам нужно показать, что
. Нам нужно показать, что 
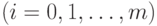 . Будем это делать индукцией по
. Будем это делать индукцией по  .
.Если  , то из целозначности многочлена
, то из целозначности многочлена  следует, что
следует, что 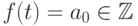 . Предположим, что
. Предположим, что  и
существование и
однозначность представления (11.11) (с целыми коэффициентами
и
существование и
однозначность представления (11.11) (с целыми коэффициентами 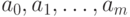 ) доказана для всех целозначных
многочленов степени меньшей
) доказана для всех целозначных
многочленов степени меньшей  . Рассматривая конечные разности
обеих частей (11.12) и используя (11.10), мы
получаем
. Рассматривая конечные разности
обеих частей (11.12) и используя (11.10), мы
получаем

 является целозначным, следовательно,
является целозначным, следовательно,  . Применяя предположение индукции к
многочлену
. Применяя предположение индукции к
многочлену 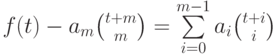 (степень которого не
превосходит
(степень которого не
превосходит 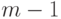 ), мы получим, что
), мы получим, что 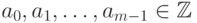 .
.Из предложения 11.3, в
частности, следует, что старший коэффициент любого целозначного многочлена  степени
степени  равен
равен 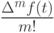 , следовательно,
, следовательно,  можно представить в виде
можно представить в виде
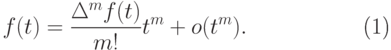 |
( 11.13) |
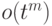 обозначает многочлен с рациональными
коэффициентами, степень которого не превосходит
обозначает многочлен с рациональными
коэффициентами, степень которого не превосходит 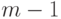 .)
.)Кроме того, поскольку  для любых
для любых 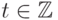 и
и 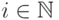 , из предложения 11.3 вытекает следующий
результат.
, из предложения 11.3 вытекает следующий
результат.
11.4. СЛЕДСТВИЕ.
Пусть  - целозначный многочлен. Тогда
- целозначный многочлен. Тогда 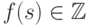 для всех
для всех  (не только достаточно
больших).
(не только достаточно
больших).
11.5. ПРЕДЛОЖЕНИЕ. Пусть 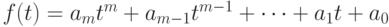 -
целозначный многочлен степени
-
целозначный многочлен степени  и
и  . Тогда существует целозначный многочлен
. Тогда существует целозначный многочлен 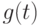 со следующими
свойствами:
со следующими
свойствами:
-
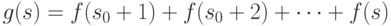 для всех
для всех 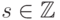 ,
, 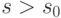 ;
; -
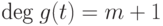 ;
; -
старший коэффициент многочлена
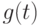 равен
равен 
ДОКАЗАТЕЛЬСТВО.
По предложению 11.3  можно представить в виде
можно представить в виде 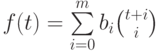 ,
где
,
где 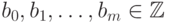 , и легко видеть, что
, и легко видеть, что  !.
Следовательно,
!.
Следовательно,
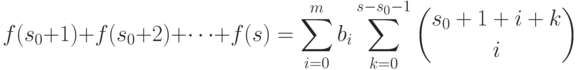
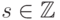 ,
, 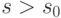 . Воспользовавшись соотношением (11.4), можно заменить внутреннюю сумму в правой части последнего
уравнения на
. Воспользовавшись соотношением (11.4), можно заменить внутреннюю сумму в правой части последнего
уравнения на  ,
следовательно,
,
следовательно,![\begin{align*}
\sum_{j=1}^{s-s_0}f(s_0+j)&=\sum_{i=0}^m b_i\left[
\binom{s+i+1}{i+1}-\binom{s_0+i+1}{i+1}\right]\\
&=\sum_{i=0}^mb_i\binom{s+i+1}{i+1}- A,
\end{align*}](/sites/default/files/tex_cache/3515d91dbffcb34552aa639d4112220a.png)
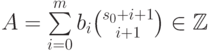 . Таким
образом, целозначный
многочлен
. Таким
образом, целозначный
многочлен 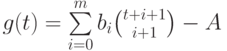 удовлетворяет всем условиям (1)-(3) (степень этого многочлена равна
удовлетворяет всем условиям (1)-(3) (степень этого многочлена равна 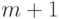 , и коэффициент при
, и коэффициент при 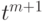 равен коэффициенту при
равен коэффициенту при 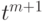 в многочлене
в многочлене 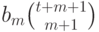 , т.е. числу
, т.е. числу 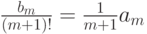 ). Предложение доказано.
). Предложение доказано.В заключение этого параграфа мы дадим решение некоторых комбинаторных задач, тесно связанных с задачей вычисления дифференциальных и разностных размерностных многочленов.
Для любых целых
чисел  и
и 
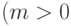 ,
, 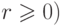 ,
пусть
,
пусть 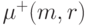 обозначает число решений уравнения
обозначает число решений уравнения
 |
( 11.14) |
 .
Пусть
.
Пусть 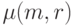 обозначает число решений уравнения
(11.14) в неотрицательных целых числах
обозначает число решений уравнения
(11.14) в неотрицательных целых числах  ,
и
,
и 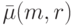 - число решений в целых
числах
- число решений в целых
числах  уравнения
уравнения |
( 11.15) |
