|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Целозначные многочлены и размерностные многочлены матриц и подмножеств в Nm
11.6. ПРЕДЛОЖЕНИЕ. В обозначениях, введенных выше,
 |
( 11.16) |
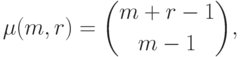 |
( 11.17) |
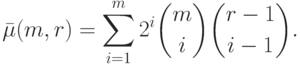 |
( 11.18) |
ДОКАЗАТЕЛЬСТВО.
Прежде всего докажем равенство (11.17). Для этого поставим в
соответствие каждому решению 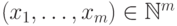 уравнения
(11.14) упорядоченное множество из
уравнения
(11.14) упорядоченное множество из  нулей
и
нулей
и  единиц,
построенное следующим образом: берем
единиц,
построенное следующим образом: берем  нулей, затем одну единицу,
затем
нулей, затем одну единицу,
затем  нулей и одну 1 и т. д. После последней единицы
берем
нулей и одну 1 и т. д. После последней единицы
берем 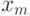 нулей. Легко видеть, что построенное соответствие взаимно
однозначно и
нулей. Легко видеть, что построенное соответствие взаимно
однозначно и 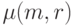 равно числу описанных выше множеств. С другой
стороны, это
число равно числу всех
равно числу описанных выше множеств. С другой
стороны, это
число равно числу всех  -элементных подмножеств
множества
-элементных подмножеств
множества 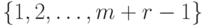 :
подмножество
:
подмножество 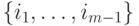
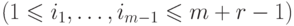 соответствует упорядоченному множеству
нулей и единиц, в котором единицы находятся на
местах
соответствует упорядоченному множеству
нулей и единиц, в котором единицы находятся на
местах 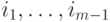 . Следовательно,
. Следовательно,  .
.
Любое решение 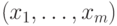 уравнения (11.14) в
положительных целых числах
соответствует решению
уравнения (11.14) в
положительных целых числах
соответствует решению 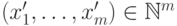 уравнения
уравнения 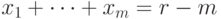 ,
где
,
где 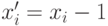
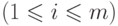 . Обратно, каждое
решение
. Обратно, каждое
решение 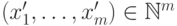 последнего уравнения
соответствует решению в положительных
целых числах
последнего уравнения
соответствует решению в положительных
целых числах 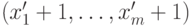 уравнения (11.14).
Следовательно,
уравнения (11.14).
Следовательно,
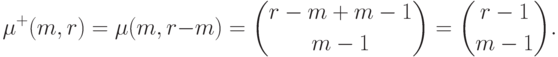
 , так как
, так как 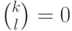 для
для  .)
.)Для доказательства равенства (11.18) заметим, что
число  -наборов
-наборов 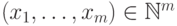 , у которых
, у которых  и все координаты
кроме
и все координаты
кроме 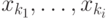
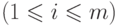 нулевые, равно
нулевые, равно 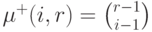 . Значит, число элементов
. Значит, число элементов 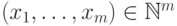 , у которых
, у которых 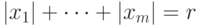 и все координаты
кроме
и все координаты
кроме 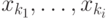 нулевые, равно
нулевые, равно 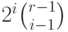 . Таким образом, существует
. Таким образом, существует 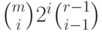 элементов
элементов 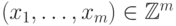 ,
таких что
,
таких что  и ровно
и ровно  координат
вектора
координат
вектора 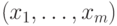 отличны от
нуля
отличны от
нуля 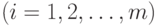 . Следовательно,
. Следовательно, 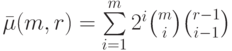 . Предложение доказано.
. Предложение доказано.
11.7. ПРЕДЛОЖЕНИЕ.
Пусть 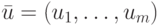 ,
, 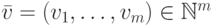 ,
, 
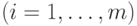 . Обозначим через
. Обозначим через 
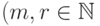 ,
, 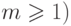 число
решений
число
решений 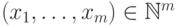 уравнения (11.14), таких,
что
уравнения (11.14), таких,
что 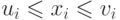
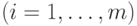 , и
пусть
, и
пусть 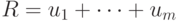 ,
, 
 . Тогда
. Тогда
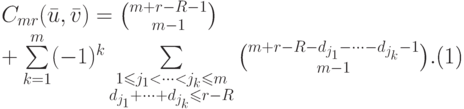 |
( 11.19) |
ДОКАЗАТЕЛЬСТВО.
Из определения  следует, что это число равно
коэффициенту при
следует, что это число равно
коэффициенту при 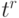 в
многочлене
в
многочлене 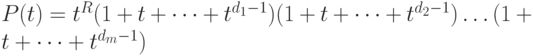 .Действительно, каждое
решение
.Действительно, каждое
решение 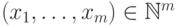
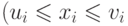 при
при 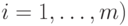 уравнения (11.14) находится во
взаимно однозначном соответствии с мономом
уравнения (11.14) находится во
взаимно однозначном соответствии с мономом 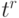 (с коэффициентом 1),
полученным разложением многочлена
(с коэффициентом 1),
полученным разложением многочлена  , если в
, если в  -х
скобках мы возьмем
множитель
-х
скобках мы возьмем
множитель 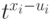
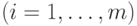 . Следовательно,
число таких мономов равно
. Следовательно,
число таких мономов равно  .
.
Поскольку 
 ,
имеем
,
имеем 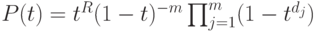 . Кроме того, так
как
. Кроме того, так
как 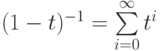 в кольце формальных
степенных рядов
в кольце формальных
степенных рядов ![\mathbb Q[[t]]](/sites/default/files/tex_cache/c90b1d43e0c7c375b6eaba8cae7ac627.png) (это равенство является непосредственным
следствием очевидного соотношения
(это равенство является непосредственным
следствием очевидного соотношения 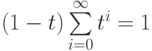 ), то
), то 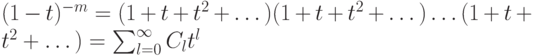 ,где (в соответствии с
вышесказанным) коэффициент
,где (в соответствии с
вышесказанным) коэффициент  равен числу
решений
равен числу
решений 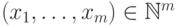 уравнения
уравнения 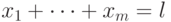 . Следовательно, (см. предложение 11.6),
. Следовательно, (см. предложение 11.6), 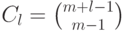 , так что
, так что 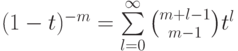 .
Это соотношение показывает, что коэффициент при
.
Это соотношение показывает, что коэффициент при 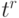 в многочлене
в многочлене
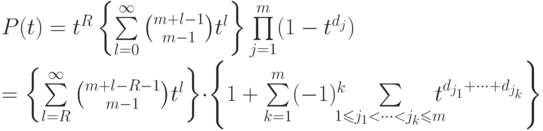
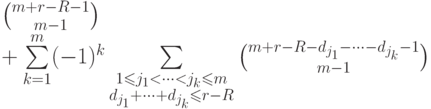
Обозначим
через 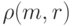 и
и 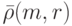 соответственно число
решений
соответственно число
решений 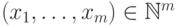 неравенства
неравенства
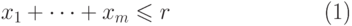 |
( 11.20) |
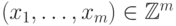 неравенства
неравенства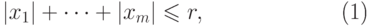 |
( 11.21) |
 .
.11.8. ПРЕДЛОЖЕНИЕ. Во введенных выше обозначениях
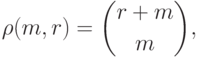 |
( 11.22) |
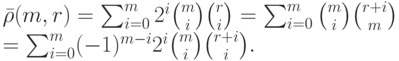 |
( 11.23) |
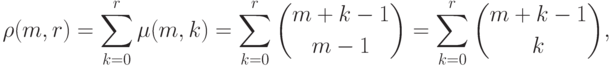
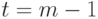 ,
,  ), что
), что  .
.Чтобы доказать (11.23), воспользуемся формулой (11.18):
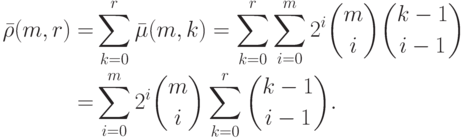
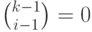 при
при 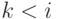 , имеем
, имеем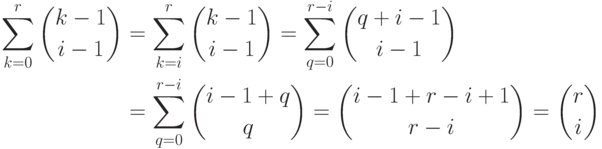
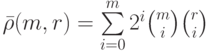 , и остальные равенства в (11.23) немедленно следуют из
(11.17) и (11.18). Предложение доказано.
, и остальные равенства в (11.23) немедленно следуют из
(11.17) и (11.18). Предложение доказано.
