НОУ ИНТУИТ | Введение в компьютерную алгебру. Лекция 3: Наибольший общий делитель и последовательности полиномиальных остатков

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 04.03.2008 | Уровень: профессионал | Доступ: платный

|

Вам нравится? Нравится 28 студентам

| Поделиться |

Поддержать программу

Расширенные алгоритмы вычисления НОД(a,b) в Z.

Наибольший общий делитель двух целых чисел обладает следую- щим важным свойством: если d = НОД(a, b), то существуют целые числа u и v, такие, что d = u · a + v · b.

5.27. УПРАЖНЕНИЕ. Доказать это свойство, пользуясь тем, что $\mathbb Z$ — кольцо главных идеалов.

Для нахождения целых чисел u и v используется метод, называемый расширенным алгоритмом Евклида.

А 5. АЛГОРИТМ (Евклида расширенный).

$\begin{align*} &\text{Дано: $a, \; b \in \mathbb N$}\\ &\text{Надо: $d \in \mathbb N, u, \; v \in \mathbb Z$}\\ &\text{Переменные: $R,X,\; Y$ — векторы элементов типа $Z$ с индексом $0..2$}\\ &\quad \quad \quad \quad \text{$q \in \mathbb Z_+$}\\ &\text{Обозначения: \quad $r \;== \;R[0], x\; == \;X[0], y \;== \;Y \;[0]$}\\ &\text{начало}\\ &\text{$X := (a,\; 1,\; 0)$}\\ &\text{$Y := (b,\; 0,\; 1)$}\\ &\text{цикл пока $y \ne 0$}\\ &\quad \text{$q := [x/y]$ \quad \quad \quad // целая часть дроби $\frac{x}{y}$}\\ &\quad \text{$R := X - q \cdot Y$}\\ &\quad \text{$X := Y$}\\ &\quad \text{$Y := R$}\\ &\text{конец цикла}\\ &\text{$(d, \;u,\; v) := X$}\\ &\text{конец}\\ \end{align*}$

Три компонента вектора X связаны соотношением:

X[0] = X[1] · a + X[2] · b.

Такое же соотношение справедливо для Y и R.

Чтобы распространить этот алгоритм на отрицательные и нулевые целые числа, достаточно заменить первые две строки следующими:

если a > 0, то X := (a, 1, 0) иначе X := (-a,-1, 0)
		если b > 0, то Y := (b, 0, 1) иначе Y := (-b, 0,-1)

5.28. УПРАЖНЕНИЕ. Доказать, что битовая сложность расширенного алгоритма Евклида равна $O(\log^2_2n)$ , где n = max(|a|, |b|).

5.29. УПРАЖНЕНИЕ. Сформулировать расширенную версию алгоритма А 1 и оценить его сложность.

До недавнего времени считалось, что расширенной версии бинарного алгоритма не существует. С.А. Абрамов и С.И. Рыбин [ 1 ] построили ее, допустив в рассмотрение вектор (0, b/2^k,-a/2^k), где 2^k — степень 2 в НОД, который можно прибавлять к другим векторам или вычитать из них.

5.30. УПРАЖНЕНИЕ. Написать расширенный бинарный алгоритм.

Эффективность вычисления НОД(a,b) в Z.

Алгоритм Евклида и бинарный алгоритм вычисления НОД являются достаточно эффективными для большинства приложений. При проектировании высокопроизводительных систем используются различные методы повышения быстродействия алгоритма вычисления НОД, в частности, алгоритм Лемера [ 9 ] .

Алгоритмы вычисления НОД(a,b) в кольцах многочленов k[x] и Z[x]

Последовательности полиномиальных остатков.

Алгоритмы А 2 и А 5 дословно переносятся на любое евклидово кольцо, в частности, на кольцо многочленов k[x] от одной переменной над произвольным полем k.

Последовательность остатков полиномов, полученная при выполнении алгоритма Евклида, называется последовательностью полиномиальных остатков ( PRS ).

Рассмотрим пример, сконцентрировав наше внимание на росте коэффициентов членов последовательности полиномиальных остатков.

6.1. ПРИМЕР. Рассмотрим полиномы p₁(x) = x³-7x+7 и p₂(x) = = 3x² - 7 как элементы евклидова кольца $\mathbb Q[x]$ . Применяя алгоритм Евклида, получаем такие последовательности:

$\begin{align*} p_1(x)&=x^3-7x+7,&&\\ p_2(x)&=3x^2-7,&&q_1(x)=(1/3)x,\\ p_3(x)&=(-14/3)x+7,&\quad&q_2(x)=(-9/14)x-27/28,\\ p_4(x)&=-1/4,&&q_3(x)=(56/3)x-28,\\ p_5(x)&=0.&& \end{align*}$

Поскольку p4(x) = -1/4, получаем НОД[p1(x), p2(x)] = 1.

Рост коэффициентов последовательности полиномиальных остатков может быть минимизирован, если каждый член, как только он получен, нормируется. В этом случае мы получаем

$\begin{align*} p_1(x)&=x^3-7x+7,&&\\ p_2(x)&=x^2-7/3,&\quad&q_1(x)=x,\\ p_3(x)&=x-3/2,&&q_2(x)=x+3/2,\\ p_4(x)&=1,&&q_3(x)=x-3/2,\\ p_5(x)&=0.&& \end{align*}$

Действительно, мы видим, что коэффициенты растут медленнее, но расплачиваемся за это вычислением НОД целых чисел на каждом шаге, чтобы максимально редуцировать дроби.

Из этого примера видно, что использовать арифметику рациональных чисел для вычисления последовательности полиномиальных остатков нецелесообразно; с одной стороны, число требуемых для максимального редуцирования коэффициентов вычислений НОД целых чисел слишком велико, и с другой стороны, отказ от редукции ведет в стремительному росту выражения.

Коэффициенты многочленов в приведенных выше примерах являются целыми числами, т. е. мы можем рассматривать эти многочлены как элементы кольца $\mathbb Z[x]$ . Поскольку это кольцо факториально (с однозначным разложением на неприводимые множители), для любых двух элементов этого кольца, не равных одновременно нулю, определен их наибольший общий делитель. С другой сторо- ны, из вложения $\mathbb Z[x] \subset \mathbb Q[x]$ следует, что мы можем рассматривать наибольший общий делитель этих же многочленов в кольце $\mathbb Q[x]$ . Как связаны между собой эти наибольшие общие делители? Одно отличие мы уже знаем: НОД в кольце $\mathbb Z[x]$ определен с точностью до знака, а в кольце $\mathbb Q[x]$ — с точностью до умножения на любое ненулевое рациональное число. Покажем, что, по существу, этим отличие и ограничивается.

6.2. ЛЕММА (Гаусса). Если коэффициенты многочлена $f \in \mathbb Z[x]$ взаимно просты в совокупности и f = g · h, где $g, h \in \mathbb Q[x]$ и НОД числителей коэффициентов каждого из многочленов g и h равен 1, то $g, h \in \mathbb Z[x]$ .

ДОКАЗАТЕЛЬСТВО. Проведем доказательство методом "от противного". Пусть $g=\sum\limits_{i=0}^na_ix^i\notin \Z[x]$ и — простое число, которое делит знаменатель какого-либо коэффициента a_i. Выберем максимальную степень числа p, которая делит знаменатель какого-либо коэффициента a_i, обозначим ее k. 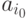Без потери общности можем обозначить i₀ такой индекс, что знаменатели коэффициентов a_i при i > i0 не делятся на p^k, а знаменатель коэффициента $a_{i_0}$ делится на p^k. Рассмотрим теперь многочлен $h(x)=\sum\limits_{j=0}^mb_jx^j.$ Пусть l — минимальная степень p, на которую делится хотя бы один коэффициент b_j (l < 0, если p делит знаменатель какого-либо коэффициента). По условию, l <= 0. Пусть j₀ — наибольшее значение индекса, на котором этот минимум достигается. Вычислим коэффициент $c_{i_0+j_0}$ при $x^{i_0+j_0}$ в произведении gh. Имеем

$c_{i_0+j_0}=a_{i_0}b_{j_0}+\sum\limits_{\substack{i+j=i_0+j_0\\i\ne i_0}}a_ib_j.$

Знаменатель первого слагаемого делится на p^k-l, знаменатель ни одного из коэффициентов под знаком суммы на это число не делится. Таким образом, знаменатель коэффициента $c_{i_0+j_0}$ делится на $p^{k-l}>1$ , что противоречит условию леммы.

Дальше >>

Введение в компьютерную алгебру

Введение в компьютерную алгебру

Наибольший общий делитель и последовательности полиномиальных остатков

Расширенные алгоритмы вычисления НОД(a,b) в Z.

Эффективность вычисления НОД(a,b) в Z.

Алгоритмы вычисления НОД(a,b) в кольцах многочленов k[x] и Z[x]

Последовательности полиномиальных остатков.

Вопросы и ответы

Студенты

Авторизоваться

Введение в компьютерную алгебру

Введение в компьютерную алгебру

Наибольший общий делитель и последовательности полиномиальных остатков

Расширенные алгоритмы вычисления НОД(a,b) в Z.

Эффективность вычисления НОД(a,b) в Z.

Алгоритмы вычисления НОД(a,b) в кольцах многочленов k[x] и Z[x]

Последовательности полиномиальных остатков.

Вопросы и ответы

Студенты