|
Можно ли, используя функцию Дирихле, построить модель пространства, в котором нет иррациональных чисел, а есть только рациональные числа? Очевидно, нельзя построить плоскость, не используя при этом иррациональные числа, так как плоскость непрерывна. Но пространство обладает бо-льшим числом измерений и может сохранить непрерывность в каком-либо одном из них. |
Элементы непрерывного математического анализа
Элементы непрерывного математического анализа
Пусть задана непрерывная функция f(x) на D(f)=[a;b]. Для такой функции справедливы следующие важные теоремы.
Теорема. Функция f(x) ограничена на D(f).
Теорема. Функция f(x) принимает на D(f) наибольшие и наименьшие значения (см. выше).
Теорема. Функция f(x) принимает на D(f) свое любое промежуточное значение C=f(c), то есть значение между A=f(a) и B=f(b), A<C<B.
Теорема. Если значения f(a)=A, f(b)=B - разных знаков, то уравнение f(x)=0 на D(f) имеет хотя бы один корень.
Если теперь задано отображение 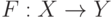 , то точка
, то точка  называется неподвижной точкой отображения F, если F(x)=x .
называется неподвижной точкой отображения F, если F(x)=x .
Существует тип уравнений, решения которых есть не числа, а функции. К таким уравнениям относятся и дифференциальные уравнения.
Дифференциальные уравнения встречаются и используются в различных областях знаний.
Рассмотрим ряд задач, которые с исторической необходимостью приводят к применению дифференциальных уравнений.
Пример (нахождение первообразной заданной функции). Если функция f(x) непрерывна на [a; b], а F(x) - ее первообразная, то, как мы показали выше, F'(x)=f(x). Мы получили уравнение, дифференциальное относительно неизвестной функции F(x). Решением его является функция (см. выше)
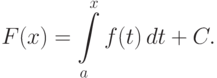
Пример (нахождение закона радиоактивного распада).
Скорость радиоактивного распада отрицательна (с течением времени масса уменьшается) и пропорциональна количеству распавшегося в данный момент вещества. Коэффициент распада - коэффициент пропорциональности  . Закон распада вещества можно описать дифференциальным уравнением вида
. Закон распада вещества можно описать дифференциальным уравнением вида 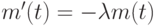 , где m(t) - количество не распавшегося к моменту времени t вещества.
, где m(t) - количество не распавшегося к моменту времени t вещества.
Пример (нахождение численности популяции). Пусть x(t) - численность некоторой биологической популяции в момент времени t, k - удельная скорость прироста особей в популяции или коэффициент рождаемости. Тогда x(t) удовлетворяет (при условии, что все остальные параметры, характеристики экологической ниши идеальны) дифференциальному уравнению вида: x'(t)=kx(t).
Пример (нахождение температуры стержня в произвольной точке). Пусть u(x,t) - температура некоторого тела (стержня) в точке x в момент времени t. Тогда уравнение, описывающее температуру в любой точке и в любой момент времени, будет иметь вид: ut=uxx, где u(x,t) - температура (функция температурных значений) в любой точке ![x\in [0;X]](/sites/default/files/tex_cache/c76e6f4d14f4f0f03a9b50f49805ea65.png) в любой момент времени
в любой момент времени ![t\in [0;T]](/sites/default/files/tex_cache/7cf9d3f04bfb927cd341ee2fa132dbf3.png) .
.
Дадим теперь определение дифференциального уравнения.
Дифференциальным уравнением называется соотношение между искомой функцией одной переменной (нескольких переменных), ее производной или дифференциалом (частными производными или дифференциалами) и независимыми переменными.
Уравнения, содержащие производные по двум и более независимым переменным, называются уравнениями в частных производных (задача 4).
Уравнения, содержащие производные лишь по одной из независимых переменных, называют обыкновенными дифференциальными уравнениями (задачи 1-3).
Обыкновенное дифференциальное уравнение можно записать в виде: F(x, y, y', y'',..., y(n))=0 (это уравнение, не разрешенное относительно неизвестной функции y(x), или обыкновенное дифференциальное уравнение в неявном виде) или y(n)=f(x, y, y', y'',..., y(n-1)) (это уравнение, решенное относительно старшей производной неизвестной функции, или обыкновенное дифференциальное уравнение в явном виде).
Порядком дифференциального уравнения называется наивысший порядок производной (производных), входящей в запись уравнения.
Пример. Все уравнения в задачах 1-3 (см. выше) - уравнения первого порядка. Уравнение в задаче 4 - второго порядка. Два последних уравнения в общем виде - уравнения n -го порядка.
Решением дифференциального уравнения называется функция, при подстановке которой в уравнение получаем тождество.
