Элементы дискретного математического анализа
Элементы дискретного математического анализа
Под численным методом ( вычислительной схемой ) решения задачи будем понимать (упрощенно) метод решения задач, который описывает последовательность этапов (шагов) решения любой такой задачи на математическом языке чисел и алгебраических действий.
Рассмотрим численное решение уравнений.
Пусть дано уравнение f(x)=0, где функция f(x) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Предполагается, что корень уравнения существует и принадлежит данному отрезку.
Численным методом решения уравнений называют метод нахождения численных значений корней уравнения с заданной точностью.
Он состоит из двух частей:
- отделение корней - нахождение интервалов, где локализованы корни, то есть в каждом таком интервале имеется ровно один корень;
- уточнение корней с заданной точностью этих отделенных корней, то есть сужение интервала, на котором отделен каждый корень уравнения, до интервала длины, не большей заданной точности нахождения корней.
Рассмотрим графический метод отделения корней. Отделение корней уравнения f(x)=0 графическим методом начинают с построения графика функции y=f(x). Абсциссы точек пересечения графика функции с осью абсцисс и есть корни уравнения. Иногда построить график функции y=f(x) достаточно сложно. Тогда уравнение f(x)=0 преобразовывают к виду f1(x)=f2(x) так, чтобы графики функций f1(x) и f2(x) было легче построить. Абсциссы точек пересечения этих графиков и есть корни уравнения.
При графическом отделении корней уравнения результат зависит от точности построения графиков. Поэтому используем аналитический численный метод отделения корней, основанный на следующем факте: если функция f(x) непрерывна на отрезке [a;b], принимает на концах этого отрезка значения противоположных знаков, а производная f'(x) на интервале (a;b) сохраняет постоянный знак, то внутри отрезка существует единственный корень уравнения f(x)=0. Этот критерий успешно применяется для уравнений f(x)=0, для которых знак производной определяется несложно.
Пример.
Рассмотрим уравнение x3-3x-0,4=0 и отрезок [-2;-1]. Функция f(x)=x3-3x-0,4 непрерывна на данном отрезке. На концах отрезка функция принимает значения противоположных знаков: f(-2)= -2,4 и f(-1)=1,6. Очевидно, что для всех 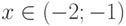 производная f'(x)>0, так как f'(x)=3x2-3=3(x-1)(x+1). Следовательно, на интервале (-2;-1) находится корень уравнения и он единственный. Аналогично можно убедиться в том, что внутри отрезков [-1;0], [1;2] находится также по одному корню.
производная f'(x)>0, так как f'(x)=3x2-3=3(x-1)(x+1). Следовательно, на интервале (-2;-1) находится корень уравнения и он единственный. Аналогично можно убедиться в том, что внутри отрезков [-1;0], [1;2] находится также по одному корню.
После отделения корней необходимо определить корни с их заданной точностью. Пусть неизвестный корень x=c уравнения f(x)=0 отделен, то есть дан отрезок [a;b], которому принадлежит только этот корень: ![c\in [a;b]](/sites/default/files/tex_cache/5204fb20e6ae6e404c8145ad0ce59a8f.png) . В качестве приближенного значения корня можно взять любую точку
. В качестве приближенного значения корня можно взять любую точку ![x\in [a;b]](/sites/default/files/tex_cache/a3b8f444cda2d67c3ab16da16fb5d9a1.png) . Очевидно, что погрешность |c-x|<b-a. Отсюда следует, что для уточнения корня с заданной точностью h нужно сужать отрезок [a;b], пока его длина не станет меньше h.
. Очевидно, что погрешность |c-x|<b-a. Отсюда следует, что для уточнения корня с заданной точностью h нужно сужать отрезок [a;b], пока его длина не станет меньше h.
Таким образом, корни можно уточнить, последовательно сужая отрезок, например, деля его пополам и выбирая половину, в которой есть отделенный корень.
Метод уточнения корня делением промежутка пополам называется методом бисекции или половинного деления .
Если корень с уравнения f(x)=0 отделен на отрезке [a;b], в качестве точки x0, которую назовем нулевым приближением корня, выберем середину отрезка: x0=(b+a)/2. Корень будет принадлежать тому из отрезков [a;x0] и [x0;b], на концах которого функция принимает значения противоположных знаков. Пусть, например, это [a;x0] то есть 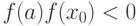 , тогда корень находится на этом промежутке, и мы далее делим пополам этот промежуток (промежуток
, тогда корень находится на этом промежутке, и мы далее делим пополам этот промежуток (промежуток ![[x_0;b]](/sites/default/files/tex_cache/c27b0cedc578e6b6ec31371ed5d58d95.png) , как не содержащий корень, выпал из дальнейшего рассмотрения). Сужают отрезок до тех пор, пока не получают отрезок длины, не превосходящий h.
, как не содержащий корень, выпал из дальнейшего рассмотрения). Сужают отрезок до тех пор, пока не получают отрезок длины, не превосходящий h.
Пример. Уточнить методом бисекции с точностью не менее h=0,01 корень уравнения f(x)=x3-3x-0,4 на [-2;-1]. Вычислим значения функции f(x) на концах отрезка [-2;-1] и выберем, в результате оценки их знаков, новую точку x={-1,5}. Таблица значений функции в серединах и на концах отрезков приведена ниже.
| N | [a;b] | x | F(x) | F(a) | F(x) | F(b) |
|---|---|---|---|---|---|---|
| 0 | [-2;-1] | -1,5 | 0,725 | - | + | + |
| 1 | [-2;-1,5] | -1,7 | -0,213 | - | - | + |
| 2 | [-1,7;-1,5] | -1,6 | 0,304 | - | + | + |
| 3 | [-1,7;-1,6] | -1,65 | 0,058 | - | + | + |
| 4 | [-1,7;-1,65] | -1,68 | -0,102 | - | - | + |
| 5 | [-1,68;-1,65] | -1,66 | 0,006 | - | + | + |
| 6 | [-1,68;-1,66] | -1,67 | -0,147 | - | - | + |
| 7 | [-1,67;-1,66] | -1,665 | -0,021 | - | - | + |
Метод деления отрезка пополам удобен тогда, когда легко вычислить значения функции на концах отрезков и точность вычисления их не будет меньше требуемой точности корня. При уточнении приближенного значения корня уравнения f(x)=0 методом деления отрезка пополам всегда имеет место сходимость метода, то есть последовательность приближенных значений корня x0,x1,x2,...,xn, ... (полусумм) будет сходиться к корню x=c.
Есть много других методов отделения и уточнения корней. Отметим среди них еще один - метод итерации. Заменим уравнение f(x)=0 равносильным уравнением x=g(x). Выберем на отрезке [a;b], содержащем только один корень x=c, приближенное значение корня. Обозначим его через x0 и назовем нулевым приближением. Каждое следующее приближение корня xn+1 при заданной точности h будем вычислять по формуле: xn+1=g(xn), n=1, 2, .... Процесс приближений к корню продолжается до тех пор, пока мы не достигнем точности корня. Критерием достижения точности может быть отклонение двух последовательных приближений не более, чем на h: |xn+1-xn|<h.
Рассмотрим второй тип численно решаемых задач - интерполирование. При решении многих задач приходится находить значения таблично заданной или очень сложно вычисляемой функции f(x) в точках x, отличных от заданных значений аргументов.
Пусть на отрезке [a;b] известны значения функции f(x) в точках x0<x1<x2<...<xn, которые называются узлами интерполяции . Требуется построить функцию F(x), совпадающую в узлах интерполяции со значениями заданной функции f(x), то есть F(x0)=f(x0), F(x1)=f(x1), ..., F(xn)=f(xn). Способ построения функции F(x), принимающей в узлах интерполяции те же значения, что и функция f(x), называется методом интерполяции или интерполирования, а функция F(x) - интерполирующей функцией, интерполянтой.
