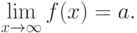Предельный переход и непрерывность
Предельный переход и непрерывность
Пусть дана некоторая последовательность перенумерованных чисел x1, x2,..., xn,..., которую обозначим коротко 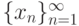 или {xn}. Эту последовательность можно записать как функцию от номера n: xn=f(n),
или {xn}. Эту последовательность можно записать как функцию от номера n: xn=f(n),  или x1=f(1), x2=f(2),..., xn=f(n),....
или x1=f(1), x2=f(2),..., xn=f(n),....
Любая последовательность будет задана, если будет указано правило образования ее членов. Последовательность, как правило, задается формулами вида xn=f(n) или xn=f(xn-1), xn=f(xn-1, xn-2) и т.д., где  .
.
Пример.Последовательность 2, 4, 8, 16, ... задана формулой xn=2n ; геометрическая прогрессия a1, a2,..., an, ... может быть определена формулой an=a1qn-1 или an=an-1q ; числа Фибоначчи 1, 1, 2, 3, 5, 8, 13, ... определяются формулами xn=xn-1+xn-2, n=3, 4, ..., x1=1, x2=1.
График числовой последовательности {xn} образуется множеством точек Mn(n;f(n)) на плоскости nOx, то есть график числовой последовательности состоит из дискретных точек.
Последовательность {xn} называется возрастающей, если выполнено условие вида 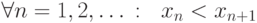 .
.
Последовательность {xn} называется убывающей, если выполнено условие вида 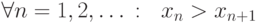 .
.
Последовательность {xn} называется не возрастающей, если выполнено условие вида 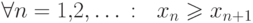 .
.
Последовательность {xn} называется не убывающей, если выполнено условие вида:  .
.
Такие последовательности называются монотонными. Остальные последовательности - не монотонные.
Рядом называется бесконечная последовательность каких-либо объектов одинаковой природы.
Пример.Ряд из чисел - числовой ряд. Ряд из функций - функциональный ряд.
Порядок следования элементов ряда - существенен. Поменяв порядок, из тех же элементов получим другой ряд.
Нас здесь интересует лишь числовой ряд и его сумма, записываемая пока формально (не конструктивно, не формализованно), то есть сумма всех членов некоторой бесконечной числовой последовательности u1, u2,..., un,..., или u1+u2+...+un+.... Этот ряд можно записать компактно в виде
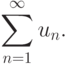
Знак  - знак "сигма" или знак суммы, последовательного суммирования всех элементов un от нижнего предела n=1 (указывается внизу, может быть как любым конечным, так и отрицательной бесконечностью) до верхнего предела
- знак "сигма" или знак суммы, последовательного суммирования всех элементов un от нижнего предела n=1 (указывается внизу, может быть как любым конечным, так и отрицательной бесконечностью) до верхнего предела  (указывается вверху, может быть любым числом, большим или равным нижнему пределу, а также положительной бесконечностью).
(указывается вверху, может быть любым числом, большим или равным нижнему пределу, а также положительной бесконечностью).
Числа un (n=1, 2, ...) называются членами ряда, а un - общим членом ряда.
Пример.В школьном курсе математики дается геометрическая бесконечно убывающая прогрессия a=aq+aq2+...+aqn-1+..., |q|<1, u1=a, u2=aq, ..., un= aqn-1. Сумма этого ряда (прогрессии), как известно из школьного курса, равна S=a/(1-q).
Пример. Гармонический ряд чисел - ряд вида: ![1+\frac 12+\frac 13+\frac 14+\dotsc + \smash[t]{\frac 1n} + \dotsc](/sites/default/files/tex_cache/9a1d83f2ac1b92b58469c7ab0861dcb4.png) . Ниже мы рассмотрим его более детально.
. Ниже мы рассмотрим его более детально.
Числовой ряд будет считаться заданным, то есть каждый его элемент будет определен однозначно, если указано правило нахождения его общего члена или дана некоторая числовая функция натурального аргумента 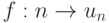 , или un=f(n).
, или un=f(n).
Пример.Если 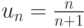 , то задан ряд
, то задан ряд 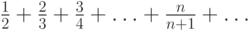 , или в компактной записи:
, или в компактной записи:

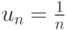 , а сам ряд - в виде
, а сам ряд - в виде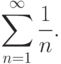
Дадим определение конечной суммы ряда и последовательности таких конечных сумм.
Конечная сумма n первых членов ряда называется его n -ой частичной суммой и обозначается через Sn:

Эта сумма находится по обычным правилам суммирования чисел. Таких сумм можно составить бесконечно много, то есть для каждого ряда можно рассматривать ряд, составленный из частичных сумм: S1, S2,... , Sn, ...
или последовательность частичных сумм, построенных для этого ряда:  .
.
Последовательность 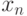 ограничена сверху, если найдется такое общее для всех членов последовательности число M, которого не превосходят все члены последовательности, то есть если выполнено следующее условие:
ограничена сверху, если найдется такое общее для всех членов последовательности число M, которого не превосходят все члены последовательности, то есть если выполнено следующее условие:
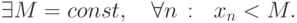
Последовательность чисел 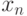 ограничена снизу, если найдется такое общее для всех членов последовательности число m, которое превосходят все члены последовательности, то есть если выполнено условие:
ограничена снизу, если найдется такое общее для всех членов последовательности число m, которое превосходят все члены последовательности, то есть если выполнено условие:
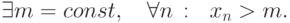
Последовательность чисел ограничена, если найдутся такие общие для всех членов последовательности числа m и M, которые удовлетворяют условию:

Число a называется пределом числовой последовательности {xn}, если существует такое малое число 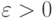 , что все члены последовательности, за исключением некоторого конечного числа первых членов, попадают в
, что все члены последовательности, за исключением некоторого конечного числа первых членов, попадают в  - окрестность числа a, то есть, в конце концов, сгущаются около точки a . Таким образом, в промежуток
- окрестность числа a, то есть, в конце концов, сгущаются около точки a . Таким образом, в промежуток 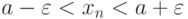 должны попасть все точки xi, i=N0, N0+1, N0+2, ... последовательности. При этом номер N0 зависит от выбранного числа
должны попасть все точки xi, i=N0, N0+1, N0+2, ... последовательности. При этом номер N0 зависит от выбранного числа  , то есть
, то есть 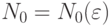 (рис. 7.1).
(рис. 7.1).
Математически существование предела последовательности можно записать в виде:
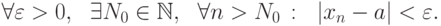
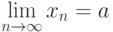 или
или  , и говорят, что
, и говорят, что 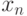 сходится к числу a. Если последовательность не имеет предела, то она называется расходящейся .
сходится к числу a. Если последовательность не имеет предела, то она называется расходящейся .Из определения предела 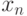 непосредственно следует: если отбросить, добавить или изменить конечное число членов последовательности, то сходимость не нарушается (то есть если сходится исходная последовательность, то сходится и измененная последовательность) и пределы исходной и полученной последовательности будут равны.
непосредственно следует: если отбросить, добавить или изменить конечное число членов последовательности, то сходимость не нарушается (то есть если сходится исходная последовательность, то сходится и измененная последовательность) и пределы исходной и полученной последовательности будут равны.
Пример.Положим, что 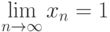 , где
, где 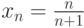 , то есть
, то есть  ,
,  ,
, 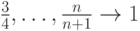 .
Этот факт легко доказывается, но мы пока берем его в качестве доказанного факта. Тогда
.
Этот факт легко доказывается, но мы пока берем его в качестве доказанного факта. Тогда 
 ,
,  :
:  . Найдем значение номера
. Найдем значение номера 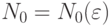 (если такой номер существует). Рассмотрим
(если такой номер существует). Рассмотрим 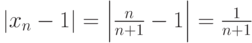 . Верно следующее соотношение:
. Верно следующее соотношение:

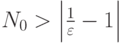 , то неравенство будет выполнено. Например, при значении
, то неравенство будет выполнено. Например, при значении 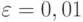 , получаем номер N0=99, то есть
, получаем номер N0=99, то есть 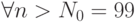 , |xn-1|<0,01. Чем меньше значение
, |xn-1|<0,01. Чем меньше значение  - тем больше значение N0. Например, если
- тем больше значение N0. Например, если 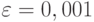 , то N0=999.
, то N0=999.Дадим теперь два эквивалентных определения предела функции: с помощью предела последовательности и с помощью соответствия малых окрестностей аргумента и значения функции. Из выполнимости одного определения следует выполнимость другого. Пусть функция y=f(x) определена  , кроме, может быть, точки x=x0, которая является предельной точкой D(f). В этой точке функция может быть не задана (не определена) или может иметь разрыв.
, кроме, может быть, точки x=x0, которая является предельной точкой D(f). В этой точке функция может быть не задана (не определена) или может иметь разрыв.
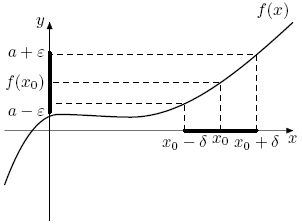
Число a называется пределом функции f(x) при  , если верно условие
, если верно условие

Число a называется пределом функции f(x) при  , если верно условие
, если верно условие
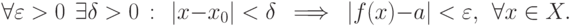

Записывают факт существования предела функции в точке в виде 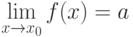 или
или 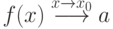 .
.
Пример.Рассмотрим функцию y=x2, ![x\in [1, 3]](/sites/default/files/tex_cache/ef8b49415261a1a881d28992de7ca1d0.png) ,
, 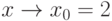 ,
, 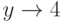 . Пусть выполнено условие
. Пусть выполнено условие 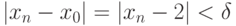 , тогда получаем
, тогда получаем

![x\in [1;3]](/sites/default/files/tex_cache/539bccb48868a9a5c480c62351b4574a.png) , то
, то ![x_n\in [1;3]](/sites/default/files/tex_cache/846737b0670e955a40344d06130da987.png) и
и 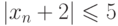 . Следовательно, можно заключить, что верно условие
. Следовательно, можно заключить, что верно условие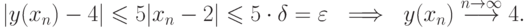
Число a называется пределом функции f(x) при 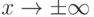 ( пределом в бесконечно удаленной точке ), если
( пределом в бесконечно удаленной точке ), если
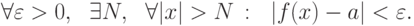
Записывают это условие (этот факт) так: