|
Можно ли, используя функцию Дирихле, построить модель пространства, в котором нет иррациональных чисел, а есть только рациональные числа? Очевидно, нельзя построить плоскость, не используя при этом иррациональные числа, так как плоскость непрерывна. Но пространство обладает бо-льшим числом измерений и может сохранить непрерывность в каком-либо одном из них. |
Предельный переход и непрерывность
Для вычисления таких пределов необходимо преобразовать (раскрыть) неопределенность  так, чтобы ее предел уже не давал неопределенность.
так, чтобы ее предел уже не давал неопределенность.
Пример.Раскроем некоторые неопределенности:
1.

2.

3.

Теорема.Если 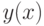 - бесконечно малая величина при
- бесконечно малая величина при  , то справедливы следующие соотношения эквивалентности:
, то справедливы следующие соотношения эквивалентности:
![\sin y\sim y, \\
\tg y \sim y, \\
\arcsin y \sim y, \\
\arctg y \sim y, \\
1-\cos y \sim y^2/2, \\
\log_a(1+y) \sim y, \\
a^y-1\sim y \ln a, \\
(1+y)^n -1 \sim ny, \\
\sqrt[n]{1+y}-1 \sim y/n.](/sites/default/files/tex_cache/9c2bb57fed5b478d7692992fb0c71ff6.png)
Пример. В частности, используя 7-е и 9-е соотношения, вычислим
Перейдем к функциям многих переменных, ограничиваясь двумя переменными: z=f(x,y).
Последовательность точек M1(x1,y1), M2(x2,y2), ..., Mn(xn,yn), ... сходится к точке M0(x0,y0), если для каждой точки Mn расстояние ее до точки M0 стремится к нулю при 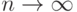 :
:  .
.
Пример.Рассмотрим пределы, вычисляемые непосредственной подстановкой координат предельной точки: 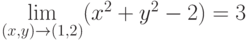 . Наоборот, функция
. Наоборот, функция  при
при  не имеет предела. Действительно, если выбрать последовательность точек {Mi} = {(x1,0), (x2,0), ..., (xn,0)}, то
не имеет предела. Действительно, если выбрать последовательность точек {Mi} = {(x1,0), (x2,0), ..., (xn,0)}, то


Пусть задана функция y=f(x) с областью определения D(f) и областью изменения E(f). Возьмем произвольную точку 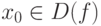 и приращение аргумента - число
и приращение аргумента - число 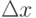 , такое, что
, такое, что  . Приращение функции в точке x0 будет равно (см. рис. 7.3):
. Приращение функции в точке x0 будет равно (см. рис. 7.3):
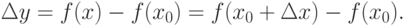
Дадим некоторые определения предела функции (различающиеся своими подходами).
Функция y=f(x) называется непрерывной в точке  , если из
, если из  следует, что
следует, что  , то есть бесконечно малым приращениям
, то есть бесконечно малым приращениям  аргумента x соответствуют бесконечно малые приращения
аргумента x соответствуют бесконечно малые приращения 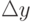 функции f(x) .
функции f(x) .
Функция y=f(x) называется непрерывной в точке 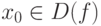 , если
, если

Сравнивая это определение с определением предела функции f(x) при 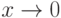 , заключаем, что можно дать эквивалентное третье определение непрерывной функции.
, заключаем, что можно дать эквивалентное третье определение непрерывной функции.
Функция y=f(x) называется непрерывной в точке 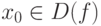 , если
, если 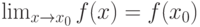 .
.
Функция, непрерывная в каждой точке 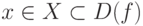 , называется непрерывной на всем множестве X .
, называется непрерывной на всем множестве X .
Пример.Функция y=x2 непрерывна в каждой точке 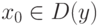 , поскольку
, поскольку 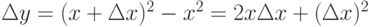 и если
и если  , то
, то 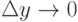 .
.
Если функция y=f(x) в точке x0 не является непрерывной, то точка x=x0 называется точкой разрыва функции .
Разрыв у функции может быть по двум причинам:
- Точка
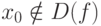 и поэтому f(x0),
и поэтому f(x0),  не определены, или
не определены, или  .
. - Из того, что
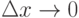 , не следует, что
, не следует, что  .
.
Пример.Пусть  . Точка x0=0 - точка разрыва, так как
. Точка x0=0 - точка разрыва, так как  . Функция
. Функция
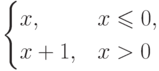
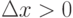 она стремится к 1, а при
она стремится к 1, а при  - стремится к 0, то есть предел в точке x0=0 не существует.
- стремится к 0, то есть предел в точке x0=0 не существует.Теорема Вейерштрасса.Функция f(x), непрерывная на [a;b], принимает на этом промежутке свое наибольшее (M) и наименьшее (m) значения.
Доказательства (строгого) этой теоремы мы не приводим. Ее суть очевидна геометрически: если график - непрерывная линия на отрезке, на этой линии есть хотя бы одна наиболее "высокая" и наиболее "низкая" точка.
Рассмотрим функцию двух переменных z=f(x,y).
Приращением функции z=f(x,y) по переменной x называется разность вида:  , а приращением по y -
, а приращением по y -  . Приращение ( полное приращение ) функции - это
. Приращение ( полное приращение ) функции - это  .
.
Непрерывное и дискретное не существуют друг без друга, переходят друг в друга, взаимно дополняют и взаимно обогащают друг друга. Дискретность невозможна без непрерывности при каких-то условиях. Непрерывность реализуется через дискретность.
Пример.Непрерывность функции определяется через дискретность - приращения аргумента и значения функции. Приращения функции невозможно рассматривать ни на одном промежутке ![[x;x+\Delta x]](/sites/default/files/tex_cache/6030e1c36b3d17b803832b713f38109f.png) изменения аргумента, не допустив непрерывности функции на этом промежутке.
изменения аргумента, не допустив непрерывности функции на этом промежутке.
Ниже мы рассмотрим и другие примеры непрерывного и дискретного, их взаимодействия и взаимообогащения.

![\displaystyle \lim\limits_{x\to 0} \frac {e^x-1}{\sqrt[3]{1-x}-1} =
\lim\limits_{x\to 0} \frac {x}{\frac {1}{3}\cdot (-x)} =-3;](/sites/default/files/tex_cache/062897704937d46396cbaa7ff2ed7e55.png)
![\displaystyle \lim\limits_{x\to 0} \frac {\arctg
\sqrt{x}}{\sin\sqrt[3]x} =
\lim\limits_{x\to 0} \frac {\sqrt{x}}{\sqrt[3]{x}} =
\lim\limits_{x\to 0} \sqrt[6]{x}=0.](/sites/default/files/tex_cache/f3ad4fb3d8dc58e5d761008db82ab0ae.png)
