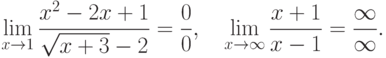НОУ ИНТУИТ | Введение в математику. Лекция 7: Предельный переход и непрерывность

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 18.04.2007 | Уровень: для всех | Доступ: свободно | ВУЗ: Кабардино-Балкарский государственный университет

|

Вам нравится? Нравится 124 студентам

| Поделиться |

Поддержать программу

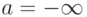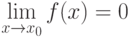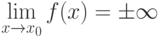Если a=0, то функция f(x) при $x\to x_0$ называется бесконечно малой . Если $a=-\infty$ ( $+\infty$ ), то функция называется бесконечно большой . Функция f(x) - бесконечно малая при $x\to x_0$ , если $\lim\limits_{x\to x_0} f(x)=0$ , и бесконечно большая при $x\to x_0$ , если $\lim\limits_{x\to x_0}f(x)=\pm \infty$ (заметим, что это не предел во введенном выше смысле, так как 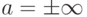$a=\pm \infty$ - не число). 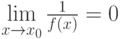Поэтому полезно пользоваться эквивалентным определением (равенством) для бесконечно больших величин: $\lim\limits_{x\to x_0}\frac {1}{f(x)}=0$ .

Бесконечно малые и большие нельзя путать с очень малыми или большими, но все же конечными, числами.

Пример.Функция f(x)=10^-100 - не бесконечно малая, f(x)=100¹⁰⁰ - не бесконечно большая.

Пример.Функция f(x)=x², 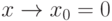$x\to x_0=0$ - бесконечно малая; f(x)=x², 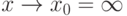$x\to x_0=\infty$ - бесконечно большая; 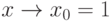$f(x)=\frac {1}{x-1}$ , $x\to x_0=1$ - бесконечно большая; f(x)=x-1, 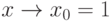$x\to x_0=1$ - бесконечно малая.

Теорема существования числа .Последовательность {x_n}, где

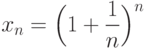
$x_n=\Bigl(1+\frac {1}{n}\Bigr)^n$

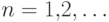$n=1{,}2, \dotsc$ сходится и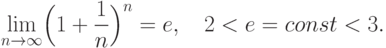

$\lim\limits_{n\to \infty} \Bigl(1+\frac 1n \Bigr)^n=e, \quad 2<e=const <3.$

Впервые ввел это число Леонард Эйлер в XVII веке. Число e - иррациональное число. Приближенное значение e=2,718281828.... С этим числом связаны экспоненциальная функция или экспонента (обозначается как e^x или 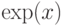$\exp(x)$ ) и натуральные логарифмы или неперовы логарифмы, предложенные Джоном Непером в XVI веке (обозначаемые как 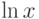$\ln x$ ). Число e играет большую роль в различных областях науки.

Пример.Рост народонаселения, рост количества бактерий, рост растений, рост некоторой суммы капитала a при процентной ставке, равной 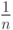$\frac 1n$ его доли, где n - количество лет, а также ряд других процессов описываются экспоненциальными функциями.

В математике часто используют так называемые замечательные пределы, то есть пределы специального вида.

Первым замечательным пределом называется предел

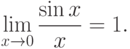
$\lim\limits_{x\to 0} \frac {\sin x}{x} =1.$

Второй замечательный предел - предел

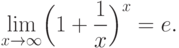
$\lim\limits_{x\to \infty} \Bigl(1+\frac 1x\Bigr)^x=e.$

Здесь e - натуральное число (натуральное основание). Из этого соотношения можно получить ряд полезных следствий:

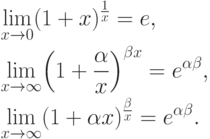
$\begin{aligned} & \lim\limits_{x\to 0} (1+x)^{\frac {1}x} =e, \\ & \lim\limits_{x\to \infty} \Bigl(1+\frac {\alpha }{x} \Bigr)^{\beta x}=e^{\alpha \beta }, \\ & \lim\limits_{x\to \infty} (1+\alpha x) ^{\frac {\beta }{x}} =e^{\alpha \beta }. \end{aligned}$

Эти пределы находят много различных приложений.

Пример.Закон роста народонаселения (который в начальный период равен k₀ и нет пока смертности и лимитирующих факторов) имеет вид

$k(t) = k_0 e^{\frac {pt}{100}}.$

Сформулируем свойства бесконечно малых и бесконечно больших величин.

Теорема.

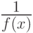Если f(x) при $x\to x_0$ - бесконечно малая, то $\frac {1}{f(x)}$ при $x\to x_0$ - бесконечно большая.
Сумма, разность и произведение конечного числа бесконечно малых при $x\to x_0$ есть бесконечно малые при $x \to x_0$ , то есть если
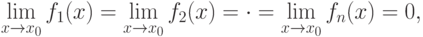
$\lim\limits_{x\to x_0} f_1(x) = \lim\limits_{x\to x_0} f_2(x) = \cdot = \lim\limits_{x\to x_0} f_n(x) = 0,$
то
$\lim\limits_{x\to x_0} [f_1(x) \pm f_2(x) \pm \dotsc \pm f_n(x)] =0, \quad \lim\limits_{x\to x_0} [f_1(x) \cdot f_2(x) \cdot \dotsc \cdot f_n(x)] =0.$
Произведение бесконечно малых (при $x \to x_0$ ) на функцию, ограниченную в окрестности точки x=x₀, есть бесконечно малая при $x \to x_0$ .
Если при $x\to x_0$ - бесконечно малая, а предел функции при $x \to x_0$ не равен нулю, то $\frac {f(x)}{g(x)}$ - бесконечно малая величина при $x \to x_0$ .
Сумма, произведение конечного числа бесконечно больших при $x\to x_0$ является бесконечно большим при $x\to x_0$ .

Случаи, когда имеем $\frac {f(x)}{g(x)}$ , где пределы числителя и знаменателя одновременно равны либо нулю, либо бесконечности, называют неопределенностями . Коротко записывают эти неопределенности так:

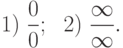
$1)\ \frac 00;\ \ 2)\ \frac {\infty}{\infty}.$

Пример.Неопределенности дают пределы вида:

$\lim\limits_{x\to 1} \frac {x^2-2x+1}{\sqrt{x+3}-2} =\frac 00, \quad \lim\limits_{x\to\infty} \frac {x+1}{x-1} =\frac \infty\infty.$

Дальше >>

Введение в математику

Предельный переход и непрерывность

Вопросы и ответы

Студенты

Авторизоваться

Введение в математику

Предельный переход и непрерывность

Вопросы и ответы

Студенты