Графы и их использование

Графы и их использование

Многие элементы и их связи удобно изображать не таблицами, а так называемыми графами. Это, хотя и часто связываемые, но все же две различные математические структуры.

Граф определяется двумя множествами V, R, где V - это множество вершин графа (множество элементов), a R - это множество ребер графа или задаваемое в зависимости от элементов V множество связей, отношений между элементами множества V . Любая пара вершин (любое ребро) может быть снабжена числом - весом ребра, которое характеризует отношение между этими вершинами, например, тесноту и важность их связи. Такие графы с весами называют взвешенными графами.

Граф, заданный геометрически (просто геометрический граф), можно изобразить кружками, отождествляемыми с элементами V и соединяющими (в соответствии с заданными отношениями R ) их линиями (ребрами). Ребра плоскостного графа могут пересекаться (зрительно) не только в вершинах, но и вне их.

Если направление связи имеет значение, то линии снабжают стрелками, и в этом случае граф называется ориентированным графом, орграфом . Если направление связи не имеет значения (для любой пары вершин равноправны направления от первой вершины ко второй и наоборот), то граф называется неориентированным графом .

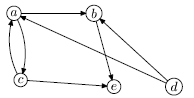
Пример. Пусть V={a, b, c, d, e}, R={r_ab, r_ac, r_ca, r_be, r_db, r_da, r_ce}, где, например, r_ab означает, что a и b связаны отношением (на геометрическом графе есть стрелка, исходящая из вершины a и входящая в вершину b ). Тогда можно построить геометрический граф (рис. 5.1).

Рис. 5.1. Ориентированный граф

Пример.Если вершины графа на рис. 5.1 отождествить с городами, а ребра - с путями, связывающими их все время "под гору", то получим ориентированный граф. Если каждое ребро снабдить стоимостью бензина на путь, то получим взвешенный граф, который можно назвать графом стоимости пути между городами (под гору) или минимальной стоимости переездов. Аналогично можно построить граф путей "в гору", который не совпадает с графом "под гору" - как по направлению стрелок, так и по весам. Если же нас интересуют только веса - длины путей, то можно изобразить единый взвешенный неориентированный граф путей.

Путь ( контур ) в графе - это последовательность дуг, связанных друг с другом так, что конец предыдущей совпадает с началом следующей. В пути каждые два соседних ребра имеют общую вершину, и никакое ребро не встречается дважды. Замкнутый путь на графе - это цикл.

Длина пути - число дуг в пути.

Расстоянием между двумя вершинами v₁ и v₂ графа G называется величина минимального по весам ребер пути из вершины v₁ в вершину v₂ .Пара вершин с ребром, их связывающим, называется дугой и обозначается (i,j) или . Начальная вершина называется истоком, началом дуги, а конечная - стоком, концом дуги. Дуга (i,j) не эквивалентна дуге (j,i). Две вершины смежные, если они соединены дугой. Две дуги смежные, если у них есть общая вершина. Вершина, обозначенная через v_k, и дуга (i,j) инцидентны, если эта вершина является началом или концом этой дуги, то есть v_k=i или v_k=j .

Связный граф - это граф, у которого для любых двух различных вершин существует путь (последовательность смежных вершин), соединяющий их.

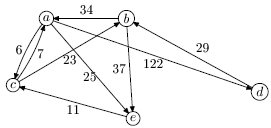
Пример.Связный взвешенный граф изображен на рис. 5.2.

Рис. 5.2. Связный взвешенный граф

Граф, заданный таблицей инцидентности, - это таблица A элементов a_ij размером n строк и m столбцов ( n - число вершин графа, m - число ребер графа, i=1,2,...,n ; j=1,2,...,m), которая заполняется по правилу: "каждой вершине графа сопоставим строку таблицы, а каждому ребру графа - столбец таблицы". Для неориентированного графа a_ij=1, если i -ая вершина инцидентна j -ой вершине, и a_ij=0 - в противном случае. Для ориентированного графа в качестве начальной вершины ставят +1, а для конечной вершины -1. Таблица инцидентности неудобна для обработки, так как она не несет прямой информации о ребрах.

Граф, заданный таблицей смежности, - это таблица B элементов b_ij размером n строк и n столбцов ( n - число вершин графа), которая заполняется по правилу: b_ij=1, если i -ая вершина смежна с j -ой вершиной, то есть существует ребро, идущее из вершины i в вершину j, и b_ij=0, - в противном случае. Таблица смежности неориентированного графа симметрична и удобнее для обработки. Если граф взвешенный, то вместо b_ij=1 в таблице проставляется вес этого ребра (i,j).

Эти способы представления имеют свои достоинства и недостатки. Основной общий недостаток обоих способов - большой объем памяти, требуемый при их запоминании, и большое число шагов для нахождения пути из одной вершины в другую.

Больший эффект имеет в этом плане представление графа списком. Будем называть списком любую упорядоченную последовательность однотипных элементов. Граф представляется списком инциденций. Этот список содержит для любой вершины i список вершин j, таких, что (неориентированный граф). Последняя запись - пара (i,j) списка часто помечается, например, словом "конец" или знаком пустого множества. Начало каждого списка хранится в отдельном списке.

Пример.Для графа, изображенного на рис. 5.1, таблица инцидентности A и таблица смежности B (она не симметрична, так как ориентирована) имеют вид:

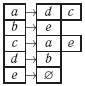
Этот же граф можно определить двумя списками: списком всех вершин (слева) и "привязанного" к каждому элементу этого списка другого списка связанных с ним вершин списка (справа):

Граф называется деревом, если он является связным и не имеет циклов, то есть замкнутых путей из одной вершины в другую, в которой все ребра попарно различны. Следовательно, для каждой пары вершин графа существует единственный соединяющий их путь.

Пример.Генеалогическое дерево - орграф. Ориентированная дуга соединяет одного члена семьи с другим, например, по принципу "родитель-сын (дочь)" (рис. 5.3).

Рис. 5.3. Генеалогическое дерево двух поколений Ивановых

В различных проблемах управления и планирования используются графы специального назначения, называемые сетевыми графиками.