НОУ ИНТУИТ | Введение в математику. Лекция 9: Интегрирование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 18.04.2007 | Уровень: для всех | Доступ: свободно | ВУЗ: Кабардино-Балкарский государственный университет

|

Вам нравится? Нравится 124 студентам

| Поделиться |

Поддержать программу

Аннотация: Рассматриваются основные математические понятия и теоремы, связанные с первообразной функции, неопределенным и определенным интегралом.

Ключевые слова: ПО, первообразной, первообразная, функция, Неопределенным интегралом, неопределенный интеграл, переменная, выражение, производная функции, интегрированием, интегрирование, дифференцирование, свойства неопределенного интеграла, дифференциал, обратная функция, метод замены переменной, суть которого в следующем, интеграл, метод интегрирования по частям, место, вычисление, DV-I, определенный интеграл, Задача о площади., площадь, график функции, отрезок, прямоугольник, равенство, интегральной суммой Дарбу, область определения, определенным интегралом, геометрический смысл определенного интеграла, Абсолютной величиной, ордината, Необходимым условием интегрируемости, Достаточным условием интегрируемости, значение, рабочее, определение, Ньютона-Лейбница, прямой, несобственными, параметр, MathCAD

Интегрирование

Выше мы рассмотрели основную задачу дифференциального исчисления - нахождение производной для любой заданной дифференцируемой функции. Обратной к этой задаче является основная задача интегрального исчисления - задача восстановления функции по ее заданной производной. Такие задачи называются обратными друг к другу или взаимообратными.

Функция F(x) называется первообразной (или примитивной) для некоторой функции f(x) на некотором заданном промежутке, если в каждой точке этого промежутка справедливо равенство F'(x)=f(x), или эквивалентно, в дифференциальной форме: dF(x)=f(x)dx .

Задача отыскания первообразной для функции f(x) решается неоднозначно: если F(x) - первообразная для f(x), то функция F(x)+C, C - const - также ее первообразная. Действительно, это следует из конструктивных правил нахождения производной суммы и постоянной, согласно которым (F(x)+C)' = F'(x) = f (x).

Теорема. Если F(x) - первообразная f(x) на промежутке X, то любая другая ее первообразная на этом промежутке может быть записана в виде F(x)+C то есть она отличается от F(x) на постоянное слагаемое; их графики параллельны.

Неопределенным интегралом от функции f(x) называется совокупность всех первообразных f(x) . Обозначается неопределенный интеграл в виде $\int f(x)\,dx = F(x)+C$ .

Здесь функция f(x) называется подынтегральной функцией; переменная x - интегральная переменная (переменная интегрирования), f(x),dx - подынтегральное выражение, f(x) - подынтегральная функция.

Пользуясь знанием производной функции F(x), можно находить ряд несложных интегралов.

Пример. По таблице производных можно восстановить интегралы следующего вида: $\int \frac 1x\,dx = \ln x+C, \\[3pt] \int 3x^2\,dx = x^3+ C, \\[3pt] \int \cos x\,dx = \sin x+C, \\[3pt] \int e^x \,dx =e^x +C, \\[3pt] \int \frac 1{x^2} \,dx =-\frac {1}{x} +C, \\[3pt] \int x^{-5} \,dx =-\frac {1}{4x^4} +C, \\[3pt] \int \sin x\,dx =-\cos x +C$ .

Задача нахождения неопределенного интеграла (первообразной) называется интегрированием функции f(x) . Интегрирование - это операция, обратная дифференцированию, и результат интегрирования может быть проверен дифференцированием. Результат дифференцирования также может быть проверен интегрированием.

Все первообразные предыдущего примера легко, по таблице производных, проверяются на правильность. Но если производная не табличного вида, результат также может быть проверен дифференцированием.

Пример.

$\int e^{-2x}\,dx = -\frac {1}{2} e^{-2x} +C , \\[2pt] \Bigl(-\frac 12 e^{-2x} +C\Bigr)' = e^{-2x}, \\[2pt] \int (\sin 3x+\cos 4x) \,dx = -\frac 13\cos 3x + \frac 14 \sin 4x +C, \\[2pt] \Bigl(-\frac 13\cos 3x+\frac 14\sin 4x +C\Bigr)' = \sin 3x +\cos 4x.$

Приведем основные свойства неопределенного интеграла.

Производная неопределенного интеграла равна подынтегральной функции: $\frac {d}{dx} \bigl(\int f(x)\,dx \bigr) =f(x)$ .
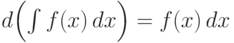Дифференциал неопределенного интеграла равен подынтегральному выражению: $d\Bigl(\int f(x)\,dx \Bigr) =f(x)\,dx$ .
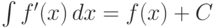Неопределенный интеграл от производной функции отличается от самой функции только на постоянную величину: $\int f'(x)\,dx = f(x) +C$ .
Постоянный множитель можно выносить за знак неопределенного интеграла. $\int kf(x)\,dx = k\int f(x)\,dx$ .
Неопределенный интеграл от суммы функции равен сумме интегралов от этих функций: $\int [f(x)+g(x)]\,dx = \int f(x)\,dx + \int g(x)\,dx$ .
Неопределенный интеграл от разности функции равен разности интегралов от этих функций: $\int [f(x)-g(x)]\,dx = \int f(x)\,dx-\int g(x)\,dx$ .

Используя таблицу производных, можно записать (и нужно запомнить) следующую таблицу неопределенных интегралов:

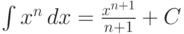
$\int x^n\,dx=\frac {x^{n+1}}{n+1}+C$ $(n\ne -1)$ .
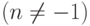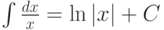$\int \frac {dx}x=\ln |x| +C$ .
$\int e^x \,dx=e^x+C$ .
$\int a^x\,dx=\frac {a^x}{\ln a} +C$ .
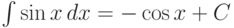$\int \sin x\,dx=-\cos x+C$ .
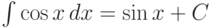$\int \cos x\,dx=\sin x+C$ .
$\int \frac {dx}{\sin^2x} =-\ctg x+C$ .
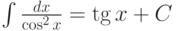$\int \frac {dx}{\cos^2x} =\tg x+C$ .
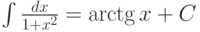$\int \frac {dx}{1+x^2} =\arctg x+C$ .
$\int \frac {dx}{\sqrt{1-x^2}} =\arcsin x+C$ .

Используя свойства неопределенных интегралов и таблицу основных интегралов, можно интегрировать некоторые функции.

Пример. Нетрудно проверить справедливость следующих равенств:

$\int 2x^3\,dx =2\int x^3\,dx =2\frac {x^4}{4} +C = \frac {x^4}{2} +C$ .
$\int\frac {dx}{x\sqrt[3]x} = \int x^{-\frac {4}{3}}\,dx = -\frac {3}{\sqrt[3] x} +C$ .
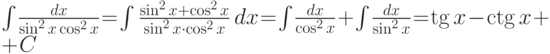$\smu{1} \int \kern-2.5pt\frac {dx}{\sin^2x \cos^2x} = \int \frac {\sin^2 x+\cos^2x}{\sin^2x \cdot \cos^2x }\,dx = \int \kern-2.5pt\frac {dx}{\cos^2x} + \kern-.5pt\int \kern-2.5pt\frac{dx}{\sin^2 x} =\tg x-\ctg x +C$ .

Правил для интегрирования произведения, частного, сложной, обратной функции в общем случае нет. Имеются лишь отдельные приемы интегрирования некоторых классов функции.

Рассмотрим наиболее часто используемый прием (метод) интегрирования - метод замены переменной, суть которого в следующем.

Если интеграл 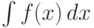$\int f(x)\,dx$ трудно вычислить, то вместо этого интеграла можно вычислить равный ему (см. свойства интеграла) интеграл 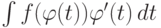$\int f(\varphi (t))\varphi '(t)\,dt$ который получается при замене в исходном интеграле переменной x по формуле 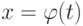$x=\varphi (t)$ . При удачном выборе этой замены последний интеграл может вычисляться легко или быть даже табличным. После того, как этот интеграл с помощью замены 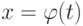$x=\varphi (t)$ будет вычислен, необходимо вернуться к "старой" переменной x, то есть подставить обратную замену $t=\varphi ^{-1}(x)$ .

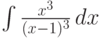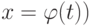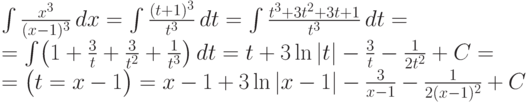Пример. $\int \frac {x^3}{(x-1)^3}\,dx$ . Замена x-1=t, откуда легко находим обратную замену x=t+1, (то есть функцию $x=\varphi (t))$ , а также необходимое для подстановки в формулу выражение для dx через новую переменную t или $dx=\varphi '(t)\,dt=(t+1)'\,dt=dt$ . В результате замены можно записать следующую цепочку равенств: $\int \frac {x^3}{(x-1)^3}\,dx = \int \frac {(t+1)^3}{t^3} \,dt = \int \frac {t^3+3t^2+3t+1}{t^3} \,dt = \\ = \int \bigl(1+\frac {3}{t}+\frac {3}{t^2}+\frac {1}{t^3} \bigr) \,dt = t + 3\ln |t| -\frac{3}{t}-\frac{1}{2t^2}+C = \\ = \bigl(t=x-1 \bigr) = x-1 + 3\ln |x-1| - \frac {3}{x-1} - \frac {1}{2(x-1)^2} +C$ .

Другим часто используемым методом вычисления интегралов является метод интегрирования по частям. Суть этого метода состоит в следующем.

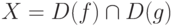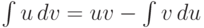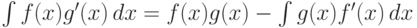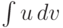Пусть функции u=f(x), v=g(x) непрерывны вместе со своими производными первого порядка на некотором промежутке $X=D(f)\cap D(g)$ . Тогда имеет место формула, называемая формулой интегрирования по частям: $\int u\,dv = uv-\int v\,du$ , или $\int f(x)g'(x) \,dx = f(x)g(x) - \int g(x)f'(x) \,dx$ . Эта формула позволяет свести вычисление некоторого более сложного интеграла $\int u\,dv$ к вычислению более простого интеграла вида 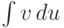$\int v\,du$ , который может быть даже табличным либо сводиться к таковому.

Основные рекомендации по интегрированию можно свести к следующим основным правилам.

В качестве функции u следует выбирать ту из функций f, g которая имеет более простую производную, а за dv принимать дифференциал той функции из них, который будет легко интегрироваться.

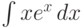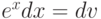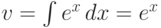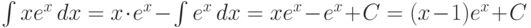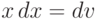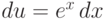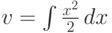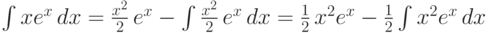Пример. Вычислим интеграл $\int xe^x\,dx$ . Пусть x=u, тогда e^x dx=dv , du=dx, $v=\int e^x\,dx=e^x$ , $\int xe^x \,dx = x\cdot e^x- \int e^x \,dx =xe^x -e^x +C=(x-1)e^x +C$ . Второй вариант выбора функции лишь усложнит вычисление, сведя вычисляемый интеграл к еще более сложному: если e^x=u, $x\,dx=dv$ , $du=e^x\,dx$ , $v=\int \frac {x^2}{2}\,dx$ , тогда $\int xe^x \,dx=\frac {x^2}2\,e^x - \int \frac {x^2}{2}\,e^x \,dx = \frac 12 \,x^2e^x - \frac 12\int x^2e^x \,dx$ .

Для получения окончательного результата приходится часто несколько раз последовательно применять формулу интегрирования по частям.

Пример. $\int x^2\sin x \,dx = \Vmatrix x^2=u, & \ \sin x \,dx = dv \\[4pt] du =2x\,dx, & \ v=\int \sin x \,dx=-\cos x \endVmatrix =\\[5pt] =-x^2\cos x+2\int \cos x\cdot x \,dx =\Vmatrix x=u, & \ du =dx, \\[4pt] \cos x\,dx =dv, & \ v=\sin x \endVmatrix = \\[4pt] =-x^2\cos x+2x\sin x +2\int \sin x \,dx = -x^2\cos x+2x\sin x+2\cos x+C$ .

Здесь в двойные вертикальные линии заключены все вычисления, которые являются подготовительными для применения формулы интегрирования по частям.

Дальше >>

Введение в математику

Интегрирование

Интегрирование

Вопросы и ответы

Студенты

Авторизоваться

Введение в математику

Интегрирование

Интегрирование

Вопросы и ответы

Студенты