НОУ ИНТУИТ | Введение в математику. Лекция 9: Интегрирование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 18.04.2007 | Уровень: для всех | Доступ: свободно | ВУЗ: Кабардино-Балкарский государственный университет

|

Вам нравится? Нравится 124 студентам

| Поделиться |

Поддержать программу

Производную любой функции, если она существует, можно найти с помощью правил дифференцирования. Для любой непрерывной функции существует первообразная, то есть неопределенный интеграл от этой функции.

Однако нет способа нахождения этой первообразной в общем случае, для произвольной функции. Более того, может оказаться, что эту первообразную вообще нельзя найти через элементарные функции. Существуют интегралы, которые не выражаются через элементарные функции с помощью конечного числа алгебраических операций и их композиций. Такие интегралы называются неквадрируемыми. Квадрируемость означает вычислимость площади (вспомним, что вычисление интеграла сводится к вычислению площади фигуры, квадратуры). К таким интегралам относятся, например, интегралы следующего вида:

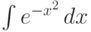$\int e^{-x^2} \,dx$ - интеграл Пуассона.
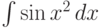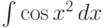$\int \sin x^2 \,dx$ , $\int \cos x^2 \,dx$ - интегралы Френеля.
$\int \frac {dx}{\ln x}$ - интегральный логарифм.
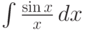$\int \frac {\sin x}{x}\,dx$ - интегральный синус.
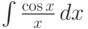$\int \frac {\cos x}{x}\,dx$ - интегральный косинус.

Хотя такие интегралы не вычисляются в элементарных функциях, но они часто встречаются на практике.

Рассмотрим одну задачу, приводящую к понятию определенного интеграла.

Задача о площади. Требуется определить площадь фигуры (криволинейная трапеция) лежащей под графиком функции y=f(x) (см., например, рис. 9.1).

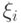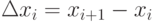Разобьем отрезок [a;b]: a=x₀<x₁<x₂<...<x_n=b. В каждом промежутке [x_i;x_i+1], i=0, 1, 2,..., n-1 выберем произвольную точку $\xi _i$ (но точку мы заранее указать не можем, это является одной из причин недетерминированности и не конструктивности интегрирования) и построим прямоугольник с высотой $f(\xi _i)$ и основанием $\Delta x_i=x_{i+1}-x_i$ . Площадь его равна: 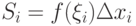$S_i=f(\xi _i)\Delta x_i$ . 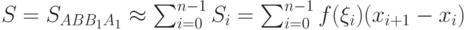Тогда можно записать приближенное равенство вида $S= S_{ABB_1A_1} \approx \sum^{n-1}_{i=0} S_i = \sum^{n-1}_{i=0} f(\xi_i)(x_{i+1} -x_i)$ .

Если $h=\max \Delta x_i$ мало при всех $0\le i\le n-1$ , то можно записать $S= \lim\limits_{h\to \0} \sum^{n-1}_{i=0} f(\xi _i)\Delta x_i , \quad \xi _i \in [x_i,x_{i+1}]$ .

Рассмотрим сумму, отвлекаясь от конкретного (физического, геометрического или др.) содержания интегрируемой функции f(x).

Пусть на [a;b] задана произвольная функция y=f(x). Разобьем [a;b]: a=x₀<x₁<...<x_n=b. В каждом [x_i;x_i+1], i=0, 1, 2,..., n-1 возьмем точку 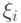$\xi_i$ . Сумма вида 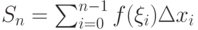$S_n = \sum^{n-1}_{i=0} f(\xi_i)\Delta x_i$ называется интегральной суммой Дарбу для функции f(x) с областью определения D(f)=[a;b] . Эта сумма зависит от выбора разбиения 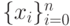$\{x_i\}^n_{i=0}$ и выбора точки 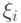$\xi_i$ на заданном отрезке [a;b].

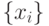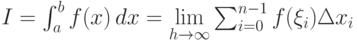Пусть $h=\max_{0\le l\le n-1} \Delta x_i$ . Если существует предел I интегральных сумм S_n при $h\to 0$ и этот предел не зависит от способа разбиения $\{x_i\}$ и от выбора точек $\xi_i\in [x_i; x_{i+1}]$ , то число I называется определенным интегралом от функции f(x) по [a;b]: $I=\int_{a}^{b} f(x)\,dx = \lim\limits_{h\to \infty} \sum^{n-1}_{i=0} f(\xi_i)\Delta x_i$ .

Из сравнения суммы в задаче о площади с интегральной суммой заключаем: геометрический смысл определенного интеграла состоит в том, что площадь фигуры (криволинейной трапеции) ограниченной линиями: y=f(x), y=0, x=a, x=b, численно равна абсолютной величине интеграла от функции f(x) в пределах от a до b .

Пример. С помощью определенного интеграла можно вычислять площадь не только криволинейной трапеции, но и более сложных фигур. Вычислим площадь фигуры, ограниченной линиями y=2-x², y=x (рис. 9.1) .

Рис. 9.1. Вычисляемая площадь — заштрихованная

Определяем точки пересечения кривых. В точке пересечения ординаты равны, отсюда получаем, что x=2-x². Решая это квадратное уравнение, находим x₁=-2, x₂=1. Тогда точками пересечения будут точки M₁(-2;-2), M₂(1;1). Искомая площадь определяется как интеграл от разности двух функций - "верхней" y=2-x² и "нижней" y=x: $S=\int_{-2}^{1} (2-x^2-x)\,dx = \Bigl[2x-\frac {x^3}{3}-\frac {x^2}{2} \Bigr]^1_{-2} = \frac 92 \ \ \text{(кв.\ единиц)}$ .

Необходимым условием интегрируемости f(x) на [a;b] является ее ограниченность на этом отрезке.

Достаточным условием интегрируемости f(x) на [a;b] в каждой точке является ее непрерывность на [a;b], возможно, за исключением конечного числа точек из [a;b] .

Отметим, что значение определенного интеграла не зависит от обозначения переменной интегрирования.

Пример. 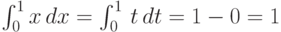$\int_{0}^{1} x\,dx = \int_{0}^{1} \,t\,dt = 1-0 =1$ .

Определение интеграла через интегральную сумму является конструктивным, но на практике интегралы через интегральные суммы не вычисляют, ибо это неудобно и громоздко. На практике используется следующее " рабочее " определение: определенным интегралом от непрерывной функции f(x) на [a;b] называется приращение ее первообразной $I=\int_{a}^{b} f(x)\,dx = F(b)-F(a)$ , где F(x) - некоторая первообразная для f(x) .

Эта формула называется формулой Ньютона-Лейбница.

Свойства определенного интеграла аналогичны свойствам неопределенного, но есть и специфические. Приведем эти свойства:

$\int_{a}^{b} f(x)\,dx =F(b)-F(a) =-[F(a)-F(b)] = - \int_{b}^{a} f(x)\,dx$ .
$\int_{a}^{b} kf(x)\,dx = k\int_{a}^{b} f(x)\,dx$ .
$\int_{a}^{b} [f(x)+g(x)]\,dx = \int_{a}^{b} f(x)\,dx+\int_{a}^{b} g(x)\,dx$ .
$\int_{a}^{b} [f(x)-g(x)]\,dx = \int_{a}^{b} f(x)\,dx- \int_{a}^{b} g(x)\,dx$ .
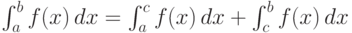$\int_{a}^{b} f(x)\,dx=\int_{a}^{c} f(x)\,dx + \int_{c}^{b} f(x)\,dx$ , где $a\le c\le b$ .
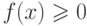Если $f (x)\ge 0$ и a<b, то $\int_{a}^{b} f(x)\,dx\ge 0$ .
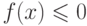Если $f (x)\le 0$ и a<b, то $\int_{a}^{b} f(x)\,dx\le 0.$
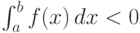Если f(x)>0 и a<b, то $\int_{a}^{b} f(x)\,dx>0$ .
Если f(x)<0 и a<b, то $\int_{a}^{b} f(x)\,dx<0$ .
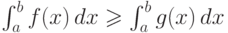Если $f(x)\ge g(x)$ , $\forall x\in [a;b]$ , то $\int_{a}^{b} f(x)\,dx\ge \int_{a}^{b} g(x)\,dx$ .

Для вычисления определенных интегралов мы, как и отмечалось выше, будем рассматривать наиболее часто используемые методы - замену переменной и интегрирование по частям.

Для определенного интеграла возможность замены вытекает из следующей теоремы.

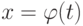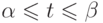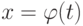Теорема (о замене переменной в определенном интеграле). Если функция f(x) непрерывна на [a;b], функция прямой замены $x=\varphi (t)$ , $\alpha \le t\le \beta$ - непрерывна вместе со своей первой производной $\varphi '(t)$ на промежутке $[\alpha ;\beta ]$ , причем все значения $x=\varphi (t)$ принадлежат [a;b], а 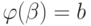$\varphi (\alpha )=a$ , $\varphi (\beta )=b$ , то тогда справедлива формула (замены переменной в определенном интеграле): $\int_{a}^{b} f(x)\,dx = \int_{\alpha}^{\beta} f(\varphi (t))\varphi '(t)\,dt$ .

Интегрирование по частям позволяет осуществлять следующая теорема.

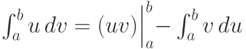Теорема (об интегрировании по частям в определенном интеграле). Если $u=\varphi (x)$ , $v=\psi(x)$ непрерывны вместе со своими первыми производными на отрезке [a;b], то справедлива формула (интегрирования по частям в определенном интеграле) $\int_{a}^{b} u\,dv = (uv)\Bigl|^b_a - \int_{a}^{b} v\,du$ , или $\int_{a}^{b} \varphi (x)\psi'(x)\,dx = \varphi (x)\psi(x)\Bigl|^b_a - \int_{a}^{b} \psi(x)\varphi '(x)\,dx$ .

Пусть функция f(x) непрерывна на [a;b]. Рассмотрим интеграл вида 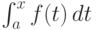$\int_{a}^{x} f(t)\,dt$ , где $a\le x\le b$ .

Этот интеграл имеет определенное для каждого значения x числовое значение, которое находится по формуле 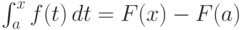$\int_{a}^{x} f(t)\,dt = F(x)-F(a)$ , зависимое от x, то есть может рассматриваться как функция от x. Обозначим интеграл $\int_{a}^{x} f(t)\,dt = \Phi(x)$ .

Отметим следующую важную теорему.

Теорема (о дифференцировании интеграла с верхним переменным пределом). Верна формула $\Phi'(x) = \frac {d}{dx} \int_{a}^{x} f(t)\,dt = f(x)$ .

Следствие. Аналогично можно утверждать, что $\frac {d}{dx} \int_{x}^{b} f(t)\,dt = -f(x), \quad a\le x\le b$ .

Если подынтегральная функция имеет разрыв или хотя бы один из пределов интегрирования бесконечен, то такие интегралы называются несобственными .

Пример. Несобственными являются интегралы $\int_{1}^{12} \frac {1}{x-5}\,dx, \quad \int_{-\infty}^{2} x\sin x\,dx, \quad \int_{0}^{1} \ln x\,dx, \quad \int_{0}^{+\infty} e^{-x}\,dx$ .

При вычислении несобственных интегралов их сводят к собственным интегралам, то есть "избавляют" подынтегральную функцию от разрывов или интеграл - от бесконечных пределов.

Пример. Первый интеграл можно вычислить следующим образом: $\int_{1}^{12} \frac {1}{x-5} \,dx = \lim\limits_{y\to 0} \Bigl(\int_{1}^{5-y} \frac {1}{x-5}\,dx + \int_{5+y}^{12} \frac {1}{x-5}\,dx\Bigr) =\\ =\lim\limits_{y\to 0} \Bigl(\ln |x-5|\, \bigr|^{x=5-y}_{x=1} \Bigr) +\lim\limits_{y\to 0} \Bigl(\ln |x-5|\, \bigr|^{x=12}_{x=5+y} \Bigr) = \\ =\lim\limits_{y\to 0} (\ln y-\ln 4+\ln 7-\ln y) = \ln 7-\ln 4 = \ln \frac74$ .

При вычислении интегралов важно правильно определить метод интегрирования, наиболее подходящий к данному интегралу (если он существует).

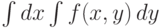Если функция двух переменных f(x,y), $a\le x\le b$ , $c\le y\le d$ сперва интегрируется по переменной y (при этом переменная x принимается за неизвестный числовой параметр), а затем полученное выражение (функция от x ) интегрируется по переменной x, то говорят о повторном интегрировании или о повторном интеграле вида $\int dx \int f(x,y)\,dy$ .

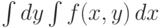Если функция двух переменных f(x,y), $a\le x\le b$ , $c\le y\le d$ сперва интегрируется по переменной x (при этом переменная y принимается за неизвестный числовой параметр), а затем полученное выражение (функция от y ) интегрируется по переменной y, то говорят о повторном интеграле вида $\int dy\int f(x,y)\,dx$ .

Аналогично рассматриваются двойной интеграл вида $\iint f(x,y)\,dx\,dy = \int dx \int f(x,y)\,dy = \int dy\int f(x,y)\,dx$ .

Выше мы отмечали ряд интегралов (Пуассона, Френеля и др.), которые не выражаются (не вычисляются) с помощью элементарных функций. Они имеют большое значение в математике. Например, интеграл Пуассона известен в теории вероятностей и математической статистике как интеграл ошибок. Численные, приближенные значения любых интегралов можно находить с помощью приближенных, численных методов (см. ниже). Имеются соответствующие, достаточно качественные математические пакеты программ для компьютера (например, MathCAD ).

Дальше >>

Введение в математику

Интегрирование

Вопросы и ответы

Студенты

Авторизоваться

Введение в математику

Интегрирование

Вопросы и ответы

Студенты