|
Можно ли, используя функцию Дирихле, построить модель пространства, в котором нет иррациональных чисел, а есть только рациональные числа? Очевидно, нельзя построить плоскость, не используя при этом иррациональные числа, так как плоскость непрерывна. Но пространство обладает бо-льшим числом измерений и может сохранить непрерывность в каком-либо одном из них. |
Элементы непрерывного математического анализа
Процесс нахождения решения называется интегрированием дифференциального уравнения .
Из задачи 1 также ясно, что решение уравнения зависит от произвольной постоянной, то есть дифференциальное уравнение может иметь бесконечное множество решений. Как правило, если дифференциальное уравнение разрешимо, то оно обладает бесконечным множеством решений, связанных друг с другом определенным правилом. Говорят о семействе решений дифференциального уравнения.
Если решение уравнения не представимо в виде явной функции, то есть представимо в виде неявной функции, то оно называется общим интегралом уравнения . График решения y(x) дифференциального уравнения называется интегральной кривой . Уравнение имеет семейство интегральных кривых, соответствующих семейству решений.
Чтобы из общего решения или из общего интеграла выделить единственное, частное решение, нужно задать дополнительные условия.
В случае уравнения первого порядка y'(x)=f(x,y) дополнительно задается условие вида y(x0)=y0, которое выделяет из семейства интегральных кривых одну, единственную - проходящую через точку M(x0;y0). Условие приведенного вида (условие начального значения искомой функции) называется условием Коши или начальным условием, а сама задача (заданное уравнение и начальное условие для выделения единственного решения из семейства решений) - задачей Коши или начальной задачей (задачей с начальным условием Коши).
В случае уравнения второго порядка вида y''(x)=f(x,y,y') дополнительно задаются условия Коши вида  .
.
Здесь для выделения единственного решения нужно уже знать и точку, и угловой коэффициент касательной к решению в этой точке. Задача с такими данными для выделения единственного решения из семейства решений также называется задачей Коши.
Вместо условий Коши для выделения единственного решения уравнения второго порядка y''(x)=f(x,y,y') дополнительно можно задавать условия вида (условия типа Дирихле)  .
Задача с такими данными для выделения единственного решения из семейства решений называется задачей Дирихле (задачей с краевыми условиями или двухточечной краевой задачей) или задачей с закрепленными концами.
.
Задача с такими данными для выделения единственного решения из семейства решений называется задачей Дирихле (задачей с краевыми условиями или двухточечной краевой задачей) или задачей с закрепленными концами.
Рассматривают и другие задачи для дифференциальных уравнений.
Наиболее важным фактом теории обыкновенных дифференциальных уравнений является теорема существования и единственности его решения, которую мы сформулируем для задачи Коши  для явного уравнения y(n)=f(x, y, y', y'',..., y(n-1)).
для явного уравнения y(n)=f(x, y, y', y'',..., y(n-1)).
Теорема(условие существования решения задачи Коши). Если функция f(z1, z2, z3,..., zn+1), связывающая независимую переменную z1(x) и зависимые переменные z2(y), z3(y') и т.д., - сама непрерывна и имеет непрерывную производную по зависимой переменной в той области их изменения, где ищется решение, то задача Коши имеет единственное непрерывное решение в этой области (при условии, что точка M(x0; y0) принадлежит этой области).
Для решения различного типа дифференциальных уравнений разработаны соответствующие методы, каждый из которых предназначен для отыскания решения определенного класса дифференциальных уравнений.
Мы рассмотрим наиболее простые классы и методы.
Дифференциальными уравнениями с разделяющимися переменными называются уравнения вида f1(x)g1(y)dx+f2(x)g2(y)dy=0,
или 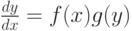 ,
где f1(x), f2(x), g1(y), g2(y), f(x), g(y) - задаваемые функции одной переменной.
,
где f1(x), f2(x), g1(y), g2(y), f(x), g(y) - задаваемые функции одной переменной.
Первое уравнение решается следующим образом:
- Разделить на произведение g1(y) f2(x) (считая, что произведение не равно нулю); тогда получим выражениеи в результате этого говорят, что переменные x и y (в этой записи) разделены;
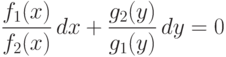
- Интегрируем полученное равенство, учитывая свойства интеграла (см. выше):
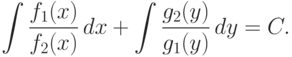
Последнее выражение есть общий интеграл уравнения с разделяющимися переменными. Если интегралы можно вычислить явно, а затем полученное соотношение однозначно разрешить относительно неизвестной y=y(x), то получим явное общее решение.
Пример.
Рассмотрим дифференциальное уравнение вида y'(x)=ky(x), где k - постоянная, а y(x) - искомая функция. Уравнение называется уравнением показательного роста (или развития системы, эволюции процесса без лимитирования со стороны окружения). К такому уравнению приводили некоторые задачи выше. Чтобы найти решение этого уравнения, поступим следующим образом. Запишем его в дифференциальной форме: 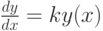 .
Разделяем переменные, то есть записываем в форме dy/y=kdx. Интегрируем (справа по x, а слева - по y ; интеграл не зависит от обозначения переменной интегрирования):
.
Разделяем переменные, то есть записываем в форме dy/y=kdx. Интегрируем (справа по x, а слева - по y ; интеграл не зависит от обозначения переменной интегрирования):
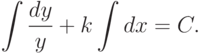
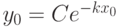 . Находим отсюда
. Находим отсюда

