НОУ ИНТУИТ | Введение в математику. Лекция 12: Элементы непрерывного математического анализа

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 18.04.2007 | Уровень: для всех | Доступ: свободно | ВУЗ: Кабардино-Балкарский государственный университет

|

Вам нравится? Нравится 124 студентам

| Поделиться |

Поддержать программу

Геометрическая прогрессия сходится при |q|<1, расходится при $|q|\ge 1$ .

Пример. Ряд 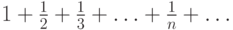$1+\frac 12+\frac {1}{3} + \dotsc + \frac{1}{n}+\dotsc$ - расходится, хотя необходимое условие сходимости ряда и выполнено. Ряд

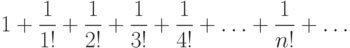
$1+\frac {1}{1!}+\frac {1}{2!}+\frac {1}{3!}+\frac {1}{4!}+ \dotsc + \frac {1}{n!}+ \dotsc$

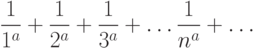
сходится, а его сумма равна S=e. Ряд

$\frac {1}{1^a} + \frac {1}{2^a} + \frac {1}{3^a} +\dotsc \frac {1}{n^a} +\dotsc$

сходится при a>1 и расходится при $a\le 1$ . Ряд

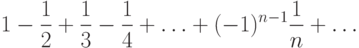
$1 - \frac 12+\frac {1}{3} -\frac {1}{4} +\dotsc + (-1)^{n-1} \frac {1}{n} +\dotsc$

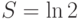сходится, сумма $S=\ln 2$ . Проверьте высказанные утверждения.

Процедура выяснения сходимости или расходимости ряда путем вычисления предела хотя и является конструктивной, но очень громоздкая и неэффективная. На практике используют другие признаки - как для выяснения сходимости, так и для расходимости ряда.

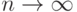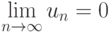Теорема(необходимый признак сходимости). Если ряд сходится, то его общий член стремится к нулю при $n\to \infty$ , $\lim\limits_{n\to \infty} u_n =0$ .

Следствие. Если условие теоремы не выполнено, то ряд расходится.

Теорема(достаточный признак сравнения). Если все члены двух рядов

$\sum\limits^\infty_{n=1} u_n =u_1+u_2+\dotsc + u_n + \dotsc, \\ \sum\limits^\infty_{n=1} v_n =v_1+v_2+\dotsc + v_n + \dotsc$

положительны (u_i>0, v_i>0, i=1,2,...) и удовлетворяют неравенству: $u_i\le v_i$ , i=1,2,..., то из сходимости второго ряда следует сходимость первого ряда, а из расходимости первого - расходимость второго.

На практике, в качестве одного из сравниваемых рядов берут заранее изученный (сходимость или расходимость которого уже доказана) "эталонный" ряд, например, геометрический ряд.

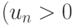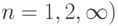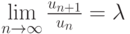Теорема (признак Даламбера). Пусть все члены ряда положительны (u_n>0 , $n=1,2,\infty)$ и существует предел $\lim\limits_{n\to \infty} \frac {u_{n+1}}{u_n} =\lambda$ . Тогда: если $\lambda <1$ , то ряд сходится; если $\lambda >1$ , то ряд расходится; если $\lambda =1$ , то признак Даламбера не дает ответа и надо использовать другие признаки (например, теорему о сравнении).

Пример. Рассмотрим ряд

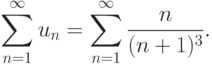
$\sum^\infty_{n=1} u_n = \sum^\infty_{n=1} \frac {n}{(n+1)^3}.$

Оценим предел Даламбера:

$\sum^\infty_{n=1} \frac {u_{n+1}}{u_n} =\lim\limits_{n\to \infty} \Bigl[\frac {n+1}{(n+2)^3} : \frac {n}{(n+1)^3}\Bigr] = \lim\limits_{n\to \infty}\Bigl(\frac {n+1}{n+2} \Bigr)^3 \cdot \lim\limits_{n\to \infty}\Bigl(\frac {n+1}{n} \Bigr) = \\ =\lim\limits_{n\to \infty}\Bigl(\frac {1+\frac {1}{n}}{1+\frac {1}{n}}\Bigr)^3 \cdot \lim\limits_{n\to \infty}\Bigl(1+\frac {1}{n} \Bigr) =1.$

Признак Даламбера не дает ответа (случай 3). Применим признак сравнения:

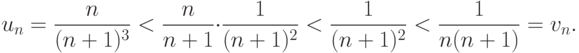
$u_n = \frac {n}{(n+1)^3} < \frac {n}{n+1}\cdot \frac {1}{(n+1)^2} < \frac {1}{(n+1)^2} < \frac {1}{n(n+1)} =v_n.$

Эталонный ряд

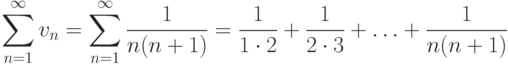
$\sum^\infty_{n=1} v_n = \sum^\infty_{n=1} \frac {1}{n(n+1)} = \frac {1}{1\cdot 2} +\frac {1}{2\cdot 3} + \dotsc + \frac {1}{n(n+1)}$

сходится. Сходится и исходный ряд.

Если члены ряда могут иметь различные знаки, то такой ряд называется знакопеременным рядом . Если знаки каждых двух последовательных членов ряда различны, то ряд называется знакочередующимся . Это ряды вида

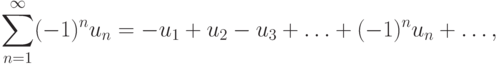
$\sum^\infty_{n=1} (-1)^n u_n = -u_1+u_2-u_3 + \dotsc + (-1)^n u_n + \dotsc,$

где u_i>0, i=1, 2,....

Теорема(признак Лейбница сходимости знакочередующегося ряда). Если абсолютные величины членов знакочередующегося ряда убывают: 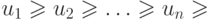$u_1\ge u_2\ge \dotsc \ge u_n \ge$ и выполнено необходимое условие сходимости ряда: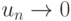 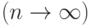$u_n\to 0$ $(n\to \infty)$ , то этот ряд сходится.

Выше мы отмечали, что ряды могут быть составлены не только из чисел.

Функциональным рядом называется ряд из функций 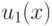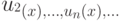u_1 (x) , $u_^2(x), \dotsc, u_n(x),\dotsc$ т.е. u₁(x)+ u₂(x)+...+u_n(x)+....

Функциональные ряды должны иметь непустое множество определения для каждого члена ряда. Они должны иметь и непустое множество D пересечений таких множеств, где определена каждая функция-слагаемое ряда. Эта область D называется областью определения ряда .

Если 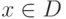$x\in D$ , то при фиксированном значении 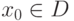$x_0\in D$ получим числовой ряд: u₁(x₀)+u₂(x₀) + ... + u_n(x₀)+.... Если этот числовой ряд сходится (расходится), то в точке x₀ функциональный ряд сходится (расходится).

Для каждого функционального ряда область определения ряда D разбивается на 2 множества D_c и D_p: для каждого 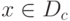$x\in D_c$ ряд сходится, а для каждого 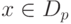$x\in D_p$ - ряд расходится, $D=D_c\cup D_p$ . Множество D_c называется областью сходимости ряда, а точки из D_c - точками сходимости.

Частным случаем функциональных рядов являются степенные ряды }:

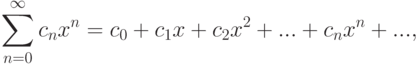
$\sum^\infty_{n=0} c_nx^n = c_0 +c_1x +c_2x^2 + ... + c_nx^n + ...,$

где

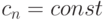
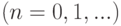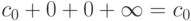называются коэффициентами ряда. Область определения степенного ряда $D=(-\infty;\infty)$ . Любой степенной ряд имеет хотя бы одну точку сходимости (x₀=0, так как ряд $c_0+0+0+\infty=c_0$ - сходится).

Теорема(признак сходимости степенного ряда). Если степенной ряд сходится при некотором значении x=x₀, 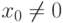$x_0\ne 0$ , то он сходится при всех x:|x|<|x₀|, причем сходится абсолютно (то есть сходится и сам исходный ряд, и ряд, составленный из модулей каждого члена исходного ряда).

Следствие. Если степенной ряд расходится при x=x₀, то он расходится и при всех x: |x|>|x₀|. Если степенной ряд сходится при некотором x=x₀, то он сходится в интервале (-|x₀|; |x₀|) и если ряд расходится при x=x₁, то он расходится и в интервале (-|x₁|; |x₁|).

Таким образом, для каждого степенного ряда есть интервал, в каждой точке которого он сходится, а вне интервала - расходится, причем на концах интервала ряд может сходиться или расходиться. Этот интервал (-R;R) называется интервалом сходимости степенного ряда, а число R - радиусом сходимости.

Для вычисления R используют предел

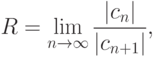
$R=\lim\limits_{n\to \infty}\frac {|c_n|}{|c_{n+1}|},$

при условии, что предел (конечный или бесконечный) существует, а все c_n

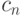отличны от нуля.

Пример. Ряд

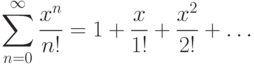
$\sum^\infty_{n=0} \frac {x^n}{n!} = 1+\frac {x}{1!} + \frac {x^2}{2!} +\dotsc$

на числовой прямой сходится, так как

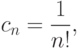
$c_n=\frac {1}{n!},$

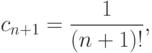
$c_{n+1}=\frac {1}{(n+1)!},$

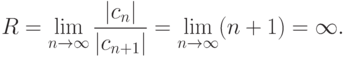
$R= \lim\limits_{n\to \infty} \frac {|c_n|}{|c_{n+1}|} = \lim\limits_{n\to \infty} (n+1) =\infty.$

Для любого $x\in (-\infty;\infty)$ сумма степенного ряда - некоторая функция f(x) :

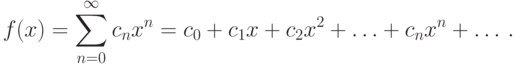
$f(x) = \sum^\infty_{n=0} c_nx^n =c_0+c_1x +c_2x^2 + \dotsc + c_nx^n + \dotsc .$

Если задана некоторая функция f(x), то разложением функции в степенной ряд называется представление f(x) в виде некоторого ряда приведенного вида. Разложение в ряд функции f(x) однозначно определяется, если однозначно найдены его коэффициенты c_n (n=0,1,...). Для нахождения коэффициентов воспользуемся теоремой.

Теорема. Степенной ряд можно почленно дифференцировать и интегрировать (от 0 до x ) внутри интервала сходимости D=({-R};R).

Продифференцируем последнее равенство по x почленно:

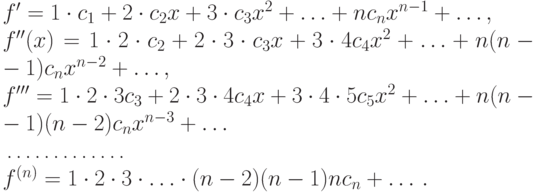
$f' = 1\cdot c_1 +2\cdot c_2x +3\cdot c_3x^2 + \dotsc + nc_nx^{n-1} + \dotsc, \\ f''(x) = 1\cdot 2\cdot c_2 +2\cdot 3\cdot c_3x +3\cdot 4c_4x^2 + \dotsc + n(n-1)c_nx^{n-2} + \dotsc, \\ f''' = 1\cdot 2\cdot 3 c_3 +2\cdot 3\cdot 4 c_4x + 3\cdot 4\cdot 5 c_5x^2 + \dotsc + n(n-1)(n-2) c_n x^{n-3} + \dotsc \\ {}&\hbox to40mm{\dotfill} \\ f^{(n)} & = 1\cdot 2\cdot 3 \cdot \dotsc \cdot (n-2)(n-1)nc_n + \dotsc\,.$

При x=0 из этих равенств поочередно получаем:

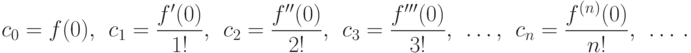
$c_0 = f(0), \ \ c_1= \frac {f'(0)}{1!}, \ \ c_2= \frac {f''(0)}{2!}, \ \ c_3= \frac {f'''(0)}{3!}, \ \ \dotsc , \ \ c_n= \frac {f^{(n)}(0)}{n!}, \ \ \dotsc\, .$

Подставляя найденные c_i (i=0,1,2,...) в искомую, пока формально записанную, формулу разложения функции f(x), получим:

$f(x) = f(0) + \frac {f'(0)}{1!}\, x + \frac {f''(0)}{2!} \, x^2 + \frac {f'''(0)}{3!} \, x^ 3+\dotsc + \frac {f^{(n)}(0)}{n!}\, x^n +\dotsc\, .$

Это разложение функции f(x) в степенной ряд называется рядом Маклорена:

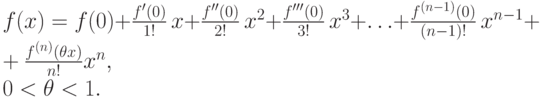
$f(x) = f(0) + \frac {f'(0)}{1!}\, x + \frac {f''(0)}{2!} \, x^2 + \frac {f'''(0)}{3!} \, x^ 3+\dotsc + \frac {f^{(n-1)}(0)}{(n-1)!}\, x^{n-1} + \frac {f^{(n)}(\theta x)}{n!}x^n, \\ 0<\theta <1.$

Пример. Разложим в ряд Маклорена f(x)=e^x. Вычислим коэффициенты

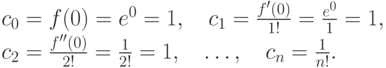
$c_0=f(0)=e^0=1, \quad c_1=\frac {f'(0)}{1!} =\frac {e^0}{1} =1, \\ c_2=\frac {f''(0)}{2!} =\frac {1}{2!} =1, \quad \dotsc, \quad c_n = \frac {1}{n!}.$

Разложение

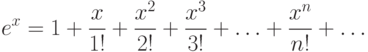
$e^x = 1+\frac {x}{1!} + \frac{x^2}{2!} + \frac {x^3}{3!} +\dotsc + \frac {x^n}{n!} + \dotsc$

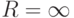для любого $x\in (-\infty;\infty)$ , $R=\infty$ .

Дальше >>

Введение в математику

Элементы непрерывного математического анализа

Вопросы и ответы

Студенты

Авторизоваться

Введение в математику

Элементы непрерывного математического анализа

Вопросы и ответы

Студенты