НОУ ИНТУИТ | Введение в математику. Лекция 12: Элементы непрерывного математического анализа

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 18.04.2007 | Уровень: для всех | Доступ: свободно | ВУЗ: Кабардино-Балкарский государственный университет

|

Вам нравится? Нравится 124 студентам

| Поделиться |

Поддержать программу

Рассмотрим еще один класс обыкновенных дифференциальных уравнений первого порядка - класс линейных уравнений в дифференциалах: $\frac {dy}{dx} =a(x) y+b(x)$ , или в производных: y'(x)+p(x)y(x)=q(x), где a(x), b(x), p(x) и q(x) - некоторые непрерывные (в промежутке, где рассматривается x ) функции, в частности, могут быть и постоянными (в этом случае уравнение называется уравнением с постоянными коэффициентами). Это уравнение линейное относительно искомой функции и ее производной и называется линейным дифференциальным уравнением . При q(x)=0 уравнение именуется линейным однородным , при $q(x)\ne 0$ уравнение именуется линейным неоднородным .

Укажем метод решения однородного уравнения.

Пусть y(x) - его решение, то есть справедливо равенство y'(x)+p(x)y(x)=0. Обозначим через v(x) одну из первообразных функций p(x) и умножим обе части равенства на отличный от нуля множитель e^v(x). Заметив, что v'(x)=p(x), получим справедливое равенство (y(x)e^v(x))'=0. Следовательно, интегрируя это равенство, получаем (y(x)e^v(x))=C, где C - произвольная постоянная. Отсюда, y(x)=Ce^-v(x). Итак, если y(x) - решение линейного однородного уравнения, то оно всегда имеет вид последней функции. Обратно, непосредственной подстановкой в уравнение этой функции можно убедиться (для этого достаточно найти первую производную и подставить ее и функцию в уравнение), что при любом значении постоянной C, функция является решением уравнения. Следовательно, y(x)=Ce^-v(x) дает множество всех решений уравнения y'(x)+p(x)y(x)=0. При начальном условии y(x₀)=y₀ из него можно выделить определенное решение конкретной задачи Коши.

Неоднородное линейное обыкновенное дифференциальное уравнение y'(x)+p(x)y(x)=q(x) сводится к уже рассмотренному случаю однородного уравнения.

В случае уравнений 2-го порядка линейное дифференциальное уравнение в общем виде записывается следующим образом: y''+p(x)y'+q(x)y=f(x). Если 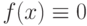$f(x)\equiv 0$ $\forall x\in [a;b]$ , (где [a,b] - отрезок, на котором рассмотрим данное уравнение), то это уравнение называется однородным, иначе - неоднородным.

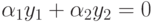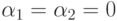Функции y₁(x) и y₂(x) называются линейно независимыми, если равенство $\alpha _1y_1+\alpha _2y_2=0$ , $\alpha _1, \alpha _2=\const$ справедливо тогда и только тогда, если $\alpha _1=\alpha _2=0$ . В противном случае (равенство справедливо лишь при $\alpha _1\ne 0$ или $\alpha _2\ne 0$ ) функции y₁, y₂ - линейно зависимы. Эти понятия аналогичны понятиям линейной зависимости и независимости векторов в R².

Теорема. Если функции y₁(x) и y₂(x) - любые линейно независимые частные решения однородного уравнения y''+p(x)y'+q(x)y=f(x), то его общее решение имеет вид: y=C₁y₁+C₂y₂, где C₁, C₂ - произвольные постоянные.

Теорема. Общее решение линейно неоднородного уравнения есть сумма его некоторого частного решения y₀(x) и общего решения соответствующего однородного уравнения.

Рассмотрим случай постоянных коэффициентов уравнения. В случае, когда коэффициенты постоянны $(p(x)\equiv p$ , $q(x)\equiv q$ , p, q=const ), уравнение примет вид y''+py'+qy=0. Из первой теоремы следует, что для получения общего решения однородного уравнения достаточно найти два его линейно независимых частных решения y₁(x) и y₂(x). Будем искать частное решение в виде y=e^kx. Тогда y'=ke^kx, y''=k²e^kx, и подставляя в уравнение, получаем

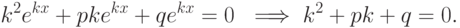
$k^2e^{kx}+pke^{kx}+qe^{kx}=0 \ \implies k^2+pk+q=0.$

Полученное квадратное уравнение называется характеристическим уравнением для линейного однородного дифференциального уравнения и может иметь два различных действительных корня k₁, k₂, или два равных корня k₁=k₂, или не иметь действительных корней.

В зависимости от этих трех случаев уравнение будет иметь частные решения определенного вида.

Рассмотрим отдельно эти случаи.

1-й случай: D=p²-4q>0, k₁, k₂ - два различных действительных корня характеристического уравнения. В этом случае функции $y_1=e^{k_1x}$ , $y_2=e^{k_2x}$ - частные решения рассматриваемого дифференциального уравнения (мы искали решение вида y=e^kx ). По первой теореме, общее решение уравнения в данном случае имеет вид

$y(x) =C_1e^{k_1x} + C_2e^{k_2x}.$

2-й случай: D=p²-4q=0, $k_1=k_2=k=-\frac {1}{2}$ . Получим только одно частное решение

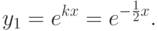
$y_1 = e^{kx} = e^{-\frac {1}{2}x}.$

За второе частное решение y₂ можно принять

$y_2=xy_1=xe^{kx} =xe^{-\frac {1}{2}x}$

. По первой теореме получаем общее решение уравнения в данном случае:

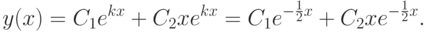
$y(x) = C_1e^{kx} + C_2xe^{kx} = C_1e^{-\frac {1}{2}x} + C_2 xe^{-\frac {1}{2}x}.$

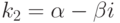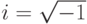3-й случай: D=p²-4q<0, действительных корней нет, но есть так называемые комплексные корни: $k_1=\alpha +\beta i$ , $k_2=\alpha -\beta i$ , где $i=\sqrt{-1}$ - так называемая мнимая единица. В этом случае частными решениями будут функции

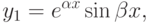
$y_1=e^{\alpha x}\sin\beta x,$

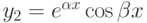
$y_2=e^{\alpha x}\cos \beta x$

Используя эти два частных решения и первую теорему, получим общее решение уравнения в данном случае: 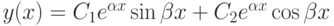$y(x) =C_1e^{\alpha x} \sin\beta x +C_2e^{\alpha x}\cos\beta x$ .

Пример. Рассмотрим уравнение y''+5y'+6y=0. Характеристическое уравнение k²+5k+6=0 имеет корни k₁=-2, k₂=-3. Решение уравнения имеет вид: y(x)=C₁e^-2x +C₂e^-3x.

Пример. Рассмотрим уравнение: y''-2y'+5y=0. Получаем характеристическое уравнение k²-2k+5=0, 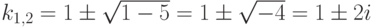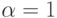$k_{1,2}=1\pm \sqrt{1-5}=1\pm \sqrt{-4}=1\pm 2i$ , $\alpha =1$ , $\beta =2$ , а, следовательно, решение имеет вид y(x)=C₁e^xsin 2x + C₂e^xcos 2x.

Рассмотрим теперь важный объект математического анализа - ряд.

Выше мы конструктивно ввели частичные конечные суммы

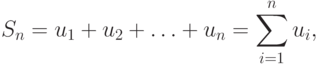
$S_n = u_1+u_2+\dotsc + u_n = \sum^n_{i=1} u_i,$

но формально не определили, как находить сумму бесконечного ряда.

Ряд u₁, u₂, ..., u_n, ... называется сходящимся, если существует конечный предел частичных сумм $\lim\limits_{n\to \infty} S_n$ . Число S называют суммой ряда и записывают так:

$S= u_1+u_2+\dotsc + u_n+ \dotsc = \sum^{\infty}_{i=1} u_i.$

Если этот предел не существует или 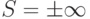$S=\pm \infty$ , то ряд называется расходящимся .

Пример. Рассмотрим геометрическую прогрессию (геометрический ряд)

$\sum^\infty_{n=1} aq^{n-1}.$

Частичные суммы -

$S_n=\sum^n_{i=1} aq^{i-1} =a+aq+aq^2 + \dotsc\break\dotsc + aq^{n-1} = \frac {aq^n-a}{q-1}$

или

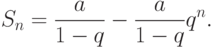
$S_n = \frac {a}{1-q} - \frac {a}{1-q} q^n.$

Возможны варианты:

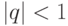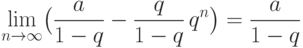
, $\displaystyle \lim\limits_{n\to \infty} \bigl(\frac {a}{1-q} - \frac {q}{1-q}\,q^n\bigr) = \frac {a}{1-q}$ $\displaystyle \lim\limits_{n\to \infty} q^n=0$ .
, $\displaystyle \lim\limits_{n\to \infty} \bigl(\frac {a}{1-q} - \frac {q}{1-q}\,q^n\bigr) = \frac {a}{1-q} \lim\limits_{n\to \infty} q^n = \frac {q}{1-q}-\infty$ - не существует предел.
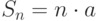, т.е. $a+a+a+\dotsc+a+\dotsc$ , $S_n = n\cdot a$ ,
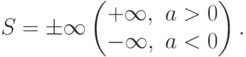
$S=\pm \infty \begin{pmatrix} +\infty, & a>0 \cr -\infty, & a<0 \cr \end{pmatrix}.$
q=-1, +a-a+... -(-1)ⁿ a + ... -, S_2n=0, S_2n+1=a - нет единственного предела (независимого от n ).