Нахождение границ
Учет направления градиента

Рис. 9.3. Нахождение границ при помощи подавления немаксимумов. Вверху - карта максимальных пикселей. Внизу - результат после пороговой фильтрации максимальных пикселей.
Будучи двухмерным вектором, градиент яркости в каждой точке характеризуется длиной и направлением. До сих пор при поиске граничных точек мы использовали только длину вектора. Проблемы, которые при этом возникли, а именно неопределенность порога  и утолщение линий, можно во многом решить, опираясь на направление градиента.
и утолщение линий, можно во многом решить, опираясь на направление градиента.
Направление градиента есть направление максимального возрастания функции. На этом основана процедура подавления немаксимумов. При этой процедуре для каждой точки рассматривается отрезок длиной в несколько пикселей, ориентированный по направлению градиента и с центром в рассматриваемом пикселе. Пиксель считается максимальным тогда и только тогда, когда длина градиента в нем максимальна среди всех длин градиентов пикселей отрезка. Граничными можно признать все максимальные пиксели с длинами градиента больше некоего порога (рис. 9.3).
Градиент яркости в каждой точке перпендикулярен границе, поэтому после подавления немаксимумов жирных линий не остается: на каждом перпендикулярном сечении жирной линии останется один пиксель с максимальной длиной градиента.
Перпендикулярность градиента яркости к границе может быть использована для прослеживания границы, начиная с некоторого граничного пикселя. Такое прослеживание используется в гистерезисной фильтрации максимальных пикселей. При проведении гистерезисной фильтрации вводят не одно, а два пороговых значения. Меньшее ( ), как и раньше, соответствует минимальной длине градиента, при которой пиксель может быть признан граничным. Большее (
), как и раньше, соответствует минимальной длине градиента, при которой пиксель может быть признан граничным. Большее (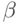 ), соответствует минимальной длине градиента, при которой пиксель может инициализировать
контур. После того как контур инициализируется в максимальном пикселе P с длиной градиента, большей
), соответствует минимальной длине градиента, при которой пиксель может инициализировать
контур. После того как контур инициализируется в максимальном пикселе P с длиной градиента, большей 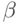 , рассматриваются каждый соседний с ним максимальный пиксель Q. Если пиксель Q имеет длину градиента, большую
, рассматриваются каждый соседний с ним максимальный пиксель Q. Если пиксель Q имеет длину градиента, большую  , и угол между векторами -
, и угол между векторами -  и
и  близок к
близок к  , то Q добавляется к контуру, и процесс рекурсивно переходит к Q. Идея гистерезисной фильтрации заключается в том, что длинный устойчивый граничный контур, скорее всего, содержит в себе пиксели с особенно большим перепадом яркости, и, начиная с такого пикселя, контур можно проследить, переходя по граничным пикселям с меньшим перепадом яркости.
, то Q добавляется к контуру, и процесс рекурсивно переходит к Q. Идея гистерезисной фильтрации заключается в том, что длинный устойчивый граничный контур, скорее всего, содержит в себе пиксели с особенно большим перепадом яркости, и, начиная с такого пикселя, контур можно проследить, переходя по граничным пикселям с меньшим перепадом яркости.
Таким образом, описаный нами алгоритм нахождения границ на основе градиента заключается в последовательном применении следующих операций:
- гауссовская сглаживающая фильтрация;
- нахождение градиента яркости в каждом пикселе;
- нахождение максимальных пикселей;
- гистерезисная фильтрация максимальных пикселей.
Этот алгоритм носит названия алгоритма Кэнни (Canny) [18]. Его результат показан на рис. 9.4. Алгоритм Кэнни является наиболее часто применяемым на сегодняшний день алгоритмом нахождения границ.



