Рекуррентные соотношения
Размещения без повторений
Имеется  различных предметов. Сколько из них можно составить
различных предметов. Сколько из них можно составить  -расстановок? При этом две расстановки считаются различными,
если они либо отличаются друг от друга хотя бы одним элементом, либо состоят из
одних и тех же элементов, но расположенных в разном порядке. Такие
расстановки называют размещениями без повторений, а их число
обозначают
-расстановок? При этом две расстановки считаются различными,
если они либо отличаются друг от друга хотя бы одним элементом, либо состоят из
одних и тех же элементов, но расположенных в разном порядке. Такие
расстановки называют размещениями без повторений, а их число
обозначают  . При составлении
. При составлении  -размещений без
повторений из
-размещений без
повторений из  предметов нам надо сделать
предметов нам надо сделать  выборов. На первом шагу можно
выбрать любой из имеющихся
выборов. На первом шагу можно
выбрать любой из имеющихся  предметов. Если этот выбор уже сделан, то на
втором шагу приходится выбирать из оставшихся
предметов. Если этот выбор уже сделан, то на
втором шагу приходится выбирать из оставшихся 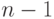 предметов. На
предметов. На  - м шагу
- м шагу  предметов. Поэтому по правилу произведения получаем, что число
предметов. Поэтому по правилу произведения получаем, что число  -размещений без повторения из
-размещений без повторения из  предметов
выражается следующим образом:
предметов
выражается следующим образом:

Перестановки
При составлении размещений без повторений из  элементов по
элементов по  мы получили расстановки, отличающиеся друг от друга и составом,
и порядком элементов. Но если брать расстановки, в которые входят все
мы получили расстановки, отличающиеся друг от друга и составом,
и порядком элементов. Но если брать расстановки, в которые входят все  элементов, то они могут отличаться друг от друга лишь порядком входящих в них
элементов. Такие расстановки называют перестановками из n
элементов, или, короче,
элементов, то они могут отличаться друг от друга лишь порядком входящих в них
элементов. Такие расстановки называют перестановками из n
элементов, или, короче,  - перестановками.
- перестановками.
Сочетания
В тех случаях, когда нас не интересует порядок элементов в комбинации, а
интересует лишь ее состав, говорят о сочетаниях. Итак,  - сочетаниями из
- сочетаниями из  элементов называют всевозможные
элементов называют всевозможные  - расстановки, составленные из
этих элементов и отличающиеся друг от друга составом, но не порядком элементов.
Число
- расстановки, составленные из
этих элементов и отличающиеся друг от друга составом, но не порядком элементов.
Число  -сочетаний, которое можно составить из
-сочетаний, которое можно составить из  элементов,
обозначают через
элементов,
обозначают через 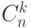 .
.
Формула для числа сочетаний получается из формулы для числа размещений. В
самом деле, составим сначала все  -сочетания из
-сочетания из  элементов, а потом переставим входящие в каждое сочетание элементы всеми
возможными способами. При этом получается, что все
элементов, а потом переставим входящие в каждое сочетание элементы всеми
возможными способами. При этом получается, что все  -размещения
из
-размещения
из  элементов, причем каждое только по одному разу. Но из
каждого
элементов, причем каждое только по одному разу. Но из
каждого  - сочетания можно сделать
- сочетания можно сделать  ! перестановок,
а число этих сочетаний равно
! перестановок,
а число этих сочетаний равно 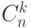 . Значит справедлива формула
. Значит справедлива формула
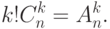
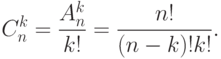
Рекуррентные соотношения
При решении многих комбинаторных задач пользуются методом сведения данной задачи к задаче, касающейся меньшего числа предметов. Метод сведения к аналогичной задаче для меньшего числа предметов называется методом рекуррентных соотношений (от латинского "recurrere" - "возвращаться").
Понятие рекуррентных соотношений проиллюстрируем классической проблемой, которая была поставлена около 1202 года Леонардо из Пизы, известным как Фибоначчи. Важность чисел Фибоначчи для анализа комбинаторных алгоритмов делает этот пример весьма подходящим.
Фибоначчи поставил задачу в форме рассказа о скорости роста популяции кроликов при следующих предположениях. Все начинается с одной пары кроликов. Каждая пара становится фертильной через месяц, после чего каждая пара рождает новую пару кроликов каждый месяц. Кролики никогда не умирают, и их воспроизводство никогда не прекращается.
Пусть 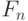 - число пар кроликов в популяции по прошествии
- число пар кроликов в популяции по прошествии  месяцев, и пусть эта популяция состоит из
месяцев, и пусть эта популяция состоит из  пар
приплода и
пар
приплода и 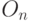 "старых" пар, то есть
"старых" пар, то есть 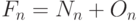 . Таким образом, в очередном месяце произойдут следующие события:
. Таким образом, в очередном месяце произойдут следующие события: 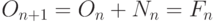 . Старая популяция в
. Старая популяция в  -й момент увеличится на число родившихся в момент времени
-й момент увеличится на число родившихся в момент времени  .
. 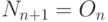 . Каждая старая пара в момент времени
. Каждая старая пара в момент времени  производит пару приплода в момент времени
производит пару приплода в момент времени 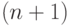 .
В последующий месяц эта картина повторяется:
.
В последующий месяц эта картина повторяется:


Объединяя эти равенства, получим следующее рекуррентное соотношение:
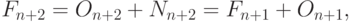
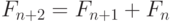 |
( 7.1) |
Выбор начальных условий для последовательности чисел Фибоначчи не важен;
существенное свойство этой последовательности определяется рекуррентным
соотношением. Будем предполагать 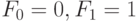 (иногда
(иногда 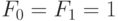 ).
).
Рассмотрим эту задачу немного иначе.
Пара кроликов приносит раз в месяц приплод из двух крольчат (самки и самца), причем новорожденные крольчата через два месяца после рождения уже приносят приплод. Сколько кроликов появится через год, если в начале года была одна пара кроликов?
Из условия задачи следует, что через месяц будет две пары кроликов. Через
два месяца приплод даст только первая пара кроликов, и получится 3 пары. А еще
через месяц приплод дадут и исходная пара кроликов, и пара кроликов, появившаяся два
месяца тому назад. Поэтому всего будет 5 пар кроликов. Обозначим через  количество пар кроликов по истечении
количество пар кроликов по истечении  месяцев с начала года. Ясно, что через
месяцев с начала года. Ясно, что через  месяцев будут эти
месяцев будут эти  пар и еще столько новорожденных пар
кроликов, сколько было в конце месяца
пар и еще столько новорожденных пар
кроликов, сколько было в конце месяца 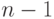 , то есть еще
, то есть еще  пар кроликов. Иными словами, имеет место рекуррентное
соотношение
пар кроликов. Иными словами, имеет место рекуррентное
соотношение
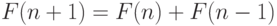 |
( 7.2) |
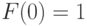 и
и 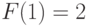 , то
последовательно находим
, то
последовательно находим
В частности, 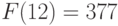 .
.
Числа  называются числами Фибоначчи. Они обладают целым рядом
замечательных свойств. Теперь выведем выражение этих чисел через
называются числами Фибоначчи. Они обладают целым рядом
замечательных свойств. Теперь выведем выражение этих чисел через  . Для
этого установим связь между числами Фибоначчи и следующей комбинаторной задачей.
. Для
этого установим связь между числами Фибоначчи и следующей комбинаторной задачей.
Найти число  последовательностей,состоящих из нулей и единиц,
в которых никакие две единицы не идут подряд.
последовательностей,состоящих из нулей и единиц,
в которых никакие две единицы не идут подряд.
Чтобы установить эту связь, возьмем любую такую последовательность и сопоставим ей пару кроликов по следующему правилу: единицам соответствуют месяцы появления на свет одной из пар "предков" данной пары (включая и исходную), а нулями - все остальные месяцы. Например, последовательность 010010100010 устанавливает такую "генеалогию": сама пара появилась в конце 11-го месяца, ее родители - в конце 7-го месяца, "дед" - в конце 5-го месяца и "прадед" - в конце второго месяца. Исходная пара кроликов тогда зашифровывается последовательностью 000000000000.
Ясно, что при этом ни в одной последовательности не могут стоять две единицы подряд - только что появившаяся пара не может, по условию, принести приплод через месяц. Кроме того, при указанном правиле различным последовательностям отвечают различные пары кроликов, и обратно, две различные пары кроликов всегда имеют разную "генеалогию", так как, по условию, крольчиха дает приплод, состоящий только из одной пары кроликов.
Установленная связь показывает, что число  -последовательностей,
обладающих указанным свойством, равно
-последовательностей,
обладающих указанным свойством, равно  .
.
Докажем теперь, что
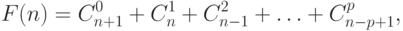 |
( 7.3) |
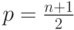 , если
, если  нечетно, и
нечетно, и  , если
, если  четно. Иными словами,
четно. Иными словами,  - целая часть числа
- целая часть числа 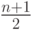 (в
дальнейшем будем обозначать целую часть числа
(в
дальнейшем будем обозначать целую часть числа  через
через  ; таким образом,
; таким образом, 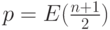 ).
).В самом деле,  - это число всех
- это число всех  -
последовательностей из 0 и 1, в которых никакие две единицы не стоят рядом.
Число же таких последовательностей, в которые входит ровно
-
последовательностей из 0 и 1, в которых никакие две единицы не стоят рядом.
Число же таких последовательностей, в которые входит ровно  единиц и
единиц и 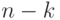 нулей, равно
нулей, равно 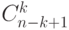 . Так как при этом
должно выполняться неравенство
. Так как при этом
должно выполняться неравенство  , то
, то  изменяется от 0 до
изменяется от 0 до 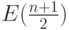 .
Применяя правило суммы, приходим к соотношению (7.3).
.
Применяя правило суммы, приходим к соотношению (7.3).
Равенство (7.3) можно доказать и иначе. Положим 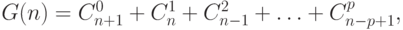 где
где 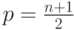 . Из равенства
. Из равенства 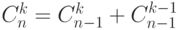 легко следует, что
легко следует, что
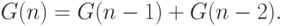 |
( 7.4) |
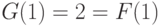 и
и 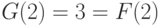 .
Так как обе последовательности
.
Так как обе последовательности  и
и  удовлетворяют рекуррентному соотношению
удовлетворяют рекуррентному соотношению 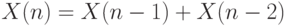 , то имеем
, то имеем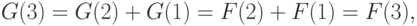
 .
.