Лекция 3: Последовательности (связанное распределение, стеки и очереди)

Связанное распределение

В "Алгоритмы на абстрактных структурах данных" даны примеры и программные реализации списков, стеков и очередей. Неудобство включения и исключения элементов при последовательном распределении происходит из-за того, что порядок следования элементов задается неявно требованием, чтобы смежные элементы последовательности находились в смежных ячейках памяти. В результате многие элементы последовательности во время включения или исключения должны передвигаться. Если это требование опущено, то можно выполнить операции включения и исключения без того, чтобы передвигать элементы последовательности. При связанном распределении последовательности (связанном списке) каждому поставлен в соответствии указатель (ссылка) , отмечающий ячейку, в которой записаны 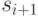и 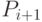. Существует также указатель 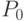, который указывает начальную ячейку последовательности, то есть ячейку с символам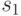и и . Все сказанное выше проиллюстрировано на рис. 3.1.

Рис. 3.1.

Здесь каждый узел состоит из двух полей. Под узлом понимается одно или несколько последовательных слов в памяти машины, которые выступают как единое целое и разделены на части, именуемые полями. В поле размещен сам элемент последовательности, а в поле 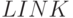- указатель на следующий за ним элемент.

Linked list - список с использованием указателей: список, в котором каждый элемент содержит указатель на следующий элемент или два указателя - на следующий и предыдущий. Поскольку для 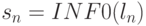следующего элемента не существует, будем использовать обозначени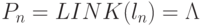е , где - пустой , или нулевой указатель . Так как точные значения для программиста не существенны, то в более общем виде связанное представление, показанное на рис. 3.1, можно изобразить так, как показано на рис.3.2.

Рис. 3.2. Другой, более употребительный, способ представления списка

Связанное представление последовательностей облегчает операции включения элемента после некоторого и исключения элемента 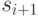, если ячейка для известна. Для этого необходимо лишь изменить значения некоторых указателей. Например, чтобы исключить элемент 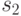из последовательности, изображенной на рис. 3.2, необходимо только положить после такой операции элемента 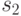в последовательности больше не будет (рис.3.3). Чтобы в последовательность, изображенную на рис. 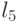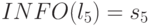3.2, включить новый элемент , необходимо только воспроизвести новый элемент в некоторой ячейке с и и присвоить 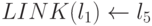.Это изображено на рис.3.4.

Рис. 3.3. Исключение элемента из связанного списка

Рис. 3.4. Включение элемента в связанный список

Использование связанного представления предполагает существование некоторого механизма, который по мере надобности поставляет новые ячейки и собирает старые ячейки, когда они освобождаются, но эта проблема выходит за рамки нашего курса.

Будем предполагать, с целью использования в различных алгоритмах, существование операции порождения ячейки get_cell ; если эта операция присутствует в правой части оператора присваивания, то она дает адрес (место) новой неиспользованной ячейки памяти. Таким образом, чтобы добавить элемент , как показано на рис. 3.4 нужно фактически использовать оператор get_cell для того чтобы найти значение 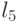. Проблему сбора ненужных ячеек памяти будем полностью игнорировать, предполагая лишь, что их каким-то образом собирают для последующего использования; такой процесс носит название сбора мусора.

Недостаток при связанном распределении - приходится тратить память на указатели 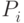. В приложениях при выборе последовательного или связанного представления нужно сначала проанализировать типы операций, которые будут выполняться над последовательностью. Если операции производятся преимущественно над случайными элементами, осуществляют поиск специфических элементов или производят упорядочение элементов, то обычно лучше применять последовательное распределение. Связанное распределение предпочтительнее, если в значительной степени используются операции включения и(или) исключения элементов, а также сцепления и (или) разбиения последовательностей.

Разновидности связанных списков

Тривиальной модификацией связанного списка, изображенного на рис 3.2, будет следующее несколько более гибкое представление последовательности: если 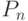указывает на 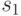, как показано на рис.3.5, то мы имеем так называемый циклический список. Такая форма списка дает возможность достигнуть любой элемент из любого другого элемента последовательности. Включение и исключение элементов здесь осуществляется так же, как и в нециклических списках, в то время как сцепление и разбиение реализуются несколько более сложно.

Рис. 3.5. Циклический список

Еще большая гибкость достигается, если использовать дважды связанный список, когда каждый элемент последовательности вместо одного имеет два связанных с ним указателя. Как показано на рис. 3.6, они указывают на элементы 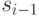и 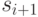. В таком списке для любого элемента имеется мгновенный прямой доступ к предыдущему и последующему элементам, в связи с чем облегчаются такие операции, как включение нового элемента перед и исключение элемента без предварительного знания его предшественника. Если есть необходимость, дважды связанный список очевидным образом можно сделать циклическим.

Рис. 3.6. Дважды связанный список